Audio per Windows, il nuovo CAD di AUDIOreview
Dopo aver trattato, nella parte prima, dell’inserimento/rilevamento dei parametri (lineari e non) e del caricamento in sospensione pneumatica, parliamo ora di quello che a vari decenni dalla sua formalizzazione è ancora di gran lunga il più “gettonato ” tra i metodi di caricamento: il “bass reflex”.
Come ormai tutti gli utilizzatori di AFW sanno, al primo lancio il programma carica il progetto delle Double Face di Gian Piero Matarazzo, in versione crossover del primo ordine. Se entriamo nella finestra di definizione del woofer e poi chiediamo di caricare l’altoparlante in bass reflex (nelle modalità viste nella prima parte con la sospensione pneumatica) avremo di fronte la finestra di figura 1, che si presenta ovvia mente un po’ più complicata rispetto al caricamento in sospensione. Anche qui abbiamo naturalmente due subpannelli che controllano rispettivamente i parametri del carica-mento ed i parametri del box, ma in più ce ne sono altrettanti per modellare la sezione di accordo e l’eventuale filtro attivo da collocare nel sistema qualora venga prescelto un allineamento misto elettrico/meccanico (come il classico B6).

Figura 1. La finestra di definizione del caricamento in bass reflex.

Figura 2. Opzioni di dimensionamento
diretto dell’allineamento reflex previste da AUDIO per Windows.
I parametri di caricamento
Il subpannello più importante è scontatamente quello dei parametri del caricamento, che sono due: il volume virtuale del box (ove il “virtuale” si riferisce al volume in cui l’altoparlante “crede” di essere rinchiuso, e che corrisponde al volume fisico moltiplicato un fattore correttivo dipendente soprattutto dalla coibentazione adottata) e la frequenza di accordo del sistema elastico costituito dal volume d’aria interno alla cassa e dalla sezione di accordo. Mentre nel caso della cassa chiusa basta richiedere un fattore di merito totale (altoparlante + cassa) pari a 0.7 (o giù di lì, a seconda delle preferenze sulla linearità della fase) per essere certi di impostare correttamente il progetto, con il reflex i due parametri fondamentali devono essere opportunamente bilanciati, altrimenti il sistema risulterà starato e la risposta irregolare e/o poco estesa.
Il criterio fondamentale di dimensionamento è stato formalizzato quarantanni or sono da Neville Thiele ed è riassunto in quella che prende appunto il nome di “tavola di Thiele”, una lista di 9 opzioni principali (in tutto sarebbero 28) di allineamento calibrate per Qt complessivi dell’altoparlante variabili tra 0.18 e 0.557 (il che, come ben sanno tutti coloro che si dilettano da anni nella progettazione di sistemi di altoparlanti, già denota come gli altoparlanti più adatti
al caricamento a reflex sono quelli dotati di buono smorzamento intrinseco). Scorrendo la tavola di Thiele nel senso dell’aumento del Qt ideale cambia la pendenza di taglio nella zona immediatamente inferiore alla frequenza di accordo, passando dal terzo ordine al quarto (che è il roll-off “naturale” del reflex, quello che governa la risposta a frequenze molto inferiori a quella di accordo). Il più famoso di tutti gli allineamenti della tavola di Thiele è probabilmente
quello centrale, denominato “B4” perché è assimilabile ad un Butterworth del quarto ordine, e la ragione di tanta notorietà è nel buon compromesso tra estensione di risposta e volume d’aria richiesto (che aumenta con il numero di Thiele, ovvero con il Qt di riferimento richiesto all’altoparlante).
Ovviamente, qualunque altoparlante può essere impiegato per realizzare uno qualunque degli allineamenti della tavola di Thiele, ma la massima linearità si ottiene solo se il Qt non si discosta troppo da quello di riferimento dell’allineamento, ed il grado di congruenza tra allineamento reflex prescelto e lo specifico trasduttore è normalmente espresso dal cosiddetto “scarto di cedevolezza”, un parametro adimensionale che rappresenta il quadrato del rapporto tra il Qt di riferimento dell’allineamento di Thiele ed il Qt dell’altoparlante impiegato.
AUDIO per Windows naturalmente permette di dimensionare con un solo click tutte e 9 le opzioni principali della tavola di Thiele (fig. 2), con il B4 corrispondente alla posizione centrale (*), ma in più prevede anche un “allineamento massimamente piatto” differente dal convenzionale B4 ed il “famoso” allineamento elettromeccanico B6. Il penultimo di quelli citati è una “estrapolazione” della tavola di Thiele dovuta a Gian Piero Matarazzo, che in termini formali si colloca tra il Qb3 n.o 4 ed il B4 (ma in modo “obliquo”, non è cioè ottenibile per interpolazione lineare) ed offre la stessa linearità del B4 ma in un volume più contenuto (e quindi – necessariamente – con una risposta leggermente meno estesa). Il B6 è invece ben noto a tutti gli “smanettoni” dei sub, essendo in pratica l’unico allineamento elettromeccanico (ovvero la cui funzione di tra sferimento complessiva è il prodotto di quella della sezione meccanica e di quella relativa al filtro passa-alto da fare precedere all’amplificatore di potenza) usato nella pratica quotidiana. Ogni qual volta l’utente richiede un allineamento di Thiele, viene calcolato e visualizzato anche lo scarto di cedevolezza, onde rendere subito evidente quanto “naturale” risulti per il woofer in questione l’opzione selezionata. In caso di scarto superiore a 4 od inferiore a 0.25 viene emesso un messaggio che avverte di come si stia cercando di forzare eccessivamente le caratteristiche intrinseche del sistema.
(*) in realtà nella versione 2.116i di AFW (quella sino ad oggi diffusa) per un errore del sottoscritto l’allineamento B4 e quello massimamente piatto proposto da G.P.M. risultano scambiati tra loro.
I parametri del mobile e della sezione di accordo
II secondo subpannello permette di descrivere/modellare il box e la coirabile bentazione, distinguendo tra le perdite dovute alla coibentazione e quelle legate al box (che a differenza del caso della sospensione pneumatica hanno effetti diversi sulla risposta e sull’impedenza, v. incorniciato di approfondimento a cura di G.P.M. in chiusura di questo articolo).
Riguardo al significato e ai valori assumibili da tali parametri vale quanto detto a proposito della sospensione pneumatica, con l’aggiunta che è normalmente improprio adottare coibentazioni rilevanti nei reflex, visto che i vantaggi che questa tecnica di caricamento offre sono tutti legati alla possibilità di far risuonare liberamente la “molla” dell’aria vincolata dal box, con quel che ne consegue in termini di freno del moto della membrana dell’altoparlante.
Il terzo subpannello è dedicato alla sezione di accordo, che può essere sia a condotto che a woofer passivo, la selezione avvenendo mediante una semplice coppia di option button. Nel caso si opti per il classico condotto è anche qui possibile inserire le perdite, che possono essere molto basse (dell’ordine di varie decine od anche centinaia, almeno ai bassi livelli) nel caso di condotti rigidi e possono altresì scendere notevolmente in caso di resistenze al moto introdotte volontariamente (come nel classico caso dei minicondotti plurimi, od in presenza di coibentazione nel condotto medesimo). In linea generale è bene non adottare mai condotti troppo piccoli (AUDIO per Windows segnala la congruenza tra il diametro minimo e la dinamica attesa, valutata grossolanamente dal volume d’aria spostabile dal woofer), perché saturano con pressioni modeste (introducendo distorsione, causando cadute di risposta e variazioni non lineari del loro Q), ma neppure troppo grandi, e non solo perché la loro lunghezza sale approssimativamente con il quadrato del diametro, ma anche perché tendono a risuonare. È proprio quest’ultimo il motivo per cui di solito si ricorre ai woofer passivi, che pur introducendo virtualmente una capacità in serie (che aumenta la pendenza in banda di transizione) ed un componente non idealmente lineare (ma anche un semplice condotto non lo è, soprattutto ad alto livello) risolvono però il problema delle risonanze alla radice.
Optando per un passivo il subpannello della sezione di accordo assume la forma di figura 3, ove compaiono i 3 parametri fondamentali (massa, diametro e risonanza in aria) ed il valore della massa da aggiungere per ottenere l’accordo desiderato (nonché i valori conseguenti della cedevolezza e della risonanza ottenuta). Nel caso di un passivo le perdite da resistenza al movimento vengono introdotte non in termini di Q equivalente (spesso non dichiarato), bensì in modo indiretto, rispondendo alla domanda “Cestello presente ?” operata da un’altra coppia di option button. Questa domanda equivale in pratica ad un’altra, ovvero “Centratore presente ?”. Se infatti c’è il centratore, e quindi nella pratica totalità dei casi anche il cestello, sussiste una componente resistiva che si oppone al moto dell’equipaggio mobile, ovvero, in termini di funzione di trasferimento, un elemento che abbassa il fattore di merito del filtro passa-alto di secondo ordine equivalente. Nel modello da noi adottato la presenza del cestello, alias centratore, equivale ad un Qm pari a 5, che sale a 20 se il centratore non c’è.

Figura 3. Il subpannello per l’inserimento dei dati del
passivo e per la visualizzazione dei risultati ottenuti in
termini di cedevolezza, risonanza e massa da aggiungere
per ottenere Vaccordo prescelto.
Il filtro elettronico opzionale
Se viene richiesto un allineamento attivo B6 allora viene visualizzato e dimensionato automaticamente anche l’ultimo subpannello (fig. 4), quello relativo al filtro elettronico passa-alto del secondo ordine da far precedere all’amplificatore di potenza. Su questo stadio non c’è molto da dire, se non che può essere ovviamente impiegato in qualsiasi altro allineamento alternativo studiato dall’utente e che, quando è presente, il massimo livello d’ingresso (MIL) diventa “massimo livello d’ingresso pesato “. Il motivo di questa variazione solo apparentemente semantica è invece sostanziale: se ad un sistema di riproduzione noi consegniamo una risposta in frequenza non lineare, in presenza di un certo segnale di ingresso il segnale di uscita risulterà attenuato od esaltato rispetto ad un fissato livello di riferimento, per cui saturerà in modo differente dallo stesso sistema eccitato da un segnale non condizionato. Se pensiamo ad esempio ad un B6, che richiede un filtro con Q pari a 2 (guadagno in tensione pari a 2 alla frequenza di taglio Ft), avremo che per F=Ft la potenza applicata varrà 4 volte quella che verrebbe applicata in assenza del filtro correttore, per cui tutto va “come se” il massimo segnale applicabile fosse 4 volte meno potente; all’opposto, nella banda attenuata del filtro elettronico (che nel particolare caso proposto inizia a 0.758 volte la Ft), la MIL pesata aumenta.

Figura 4. Subpannello per l’inserimento dei dati del filtro opzionale passa-alto del 11 ordine, che viene dimensionato automaticamente qualora l’allineamento prescelto sia il B6.
Naturalmente, la MOL non viene in alcun modo interessata da quanto viene fatto a monte dell’alto parlante.

Figura 5. Se si introduce o modifica un filtro attivo, all’uscita del quadro di definizione del caricamento reflex viene chiesto se si vuole inserire tale filtro nel blocco dei filtri attivi che competono alla via interessata. Se la risposta è positiva il blocco viene riarrangiato automaticamente.
Quando viene richiesto un allineamento con filtro attivo, all’uscita dal quadro di definizione del caricamento reflex viene richiesto (fig. 5) se si vuole inserire quel filtro nel blocco dei filtri attivi che compete all’amplificatore che alimenta l’altoparlante caricato in reflex. Sia che la risposta sia positiva sia che sia negativa, nella finestra di definizione del trasduttore comparirà la sola risposta meccanica dell’altoparlante (mentre nella finestra di caricamento compariva la risposta totale dell’allineamento); ovviamente, se si è risposto di sì ed il filtro è stato inserito, quando si va nel quadro delle simulazioni globali la risposta simulata sarà quella totale (meccanica + filtro).
di Fabrizio Montanucci
La sospensione pneumatica come modello acustico
La sospensione pneumatica o cassa chiusa che dir si voglia rappresenta il più semplice dei carichi acustici, ovvero quello più facile da realizzare e, sotto diversi aspetti, anche quello più corretto dal punto di vista musicale.
Spesso si sente parlare di velocità della gamma più bassa e profonda e si attribuisce alla sospensione pneumatica la maggiore velocità raggiungibile, senza però chiarirne il significato. In effetti occorre precisare che non ha alcun senso parlare di velocità in gamma bassa: innanzitutto non esistono in natura basse frequenze “veloci”, ma soltanto basse frequenze, prodotte da masse in movimento, per l’eccitazione meccanica di grosse membrane (percussioni), per la combinazione di camere risonanti e corde (contrabbasso) o per risonanza dell’aria (canne d’organo). In tutti i tre casi è lecito pensare che non esistano requisiti per avere alte velocità, ma è ragionevole supporre che i rapporti di ampiezza e di fase acustica tra la fondamentale e le armoniche debbano essere rispettati. Dal punto di vista analitico la risposta ai transienti non tiene conto della massa mobile leggera o del complesso magnetico sovradimensionato ma soltanto della banda passante del woofer con il suo carico e col suo filtro crossover passa-basso.
Determinante per la qualità del suono viceversa è lo smorzamento acustico totale del sistema, ove con tale denominazione si definisce l’inviluppo della risposta del passa-alto naturale non tanto del solo diffusore, ma appunto di tutto il sistema: amplificatore, cavi di collegamento e diffusore. Solo le basse frequenze ben smorzate anche se non estese all’estremo udibile sono denominate “veloci” per il corretto andamento della fondamentale e delle sue armoniche. Anni fa campionammo una forte percussione sulla grancassa di una batteria e ne facemmo una analisi spettrale delle prime armoniche, attribuibili ad un ipotetico woofer non limitato dal crossover, che comparata alla stessa percussione riprodotta da un diffusore ne mostrava limiti ed alterazioni, con le immancabili variazioni che potevano essere ricondotte allo smorzamento ed alla diversa ampiezza delle armoniche. È da allora che ci ripetiamo che occorre parlare di smorzamento, e tutt’al più di corretto andamento della fase più che di velocità.
Non a caso i risultati migliori in termini di smorzamento e senso realistico delle basse frequenze vengono ottenuti da subwoofer con controlli che in qualche modo ne consentano la regolarizzazione della fase acustica, come ad esempio avviene con il pilotaggio in corrente.
La sospensione come modello matematico
AFW utilizza un modello matematico relativamente semplice per il calcolo della risposta e dell’impedenza della sospensione pneumatica, che tuttavia permette una quantificazione molto precisa delle grandezze in gioco e dell’alterazione della risposta dovuta alle perdite. Come abbiamo visto nelle puntate precedenti possiamo ottenere il modello matematico completo della sospensione pneumatica stravolgendo appena quello caratteristico di un altoparlante in aria libera. In Fig. 1 possiamo vedere come al circuito equivalente acustico dell’altoparlante è stato aggiunto il modello matematico del volume chiuso nella sua forma più complessa. Riconosciamo Ral, che è la resistenza dovuta alle perdite per fessurazione del mobile, e Rab, che simula le perdite per assorbimento sia del box che dell’eventuale assorbente immesso. In Fig. 2 invece possiamo vedere come il complesso modello di prima sia stato ridotto con il metodo dei sotto-sottomoduli.

Fig. 1. Modello acustico completo della sospensione pneumatica.
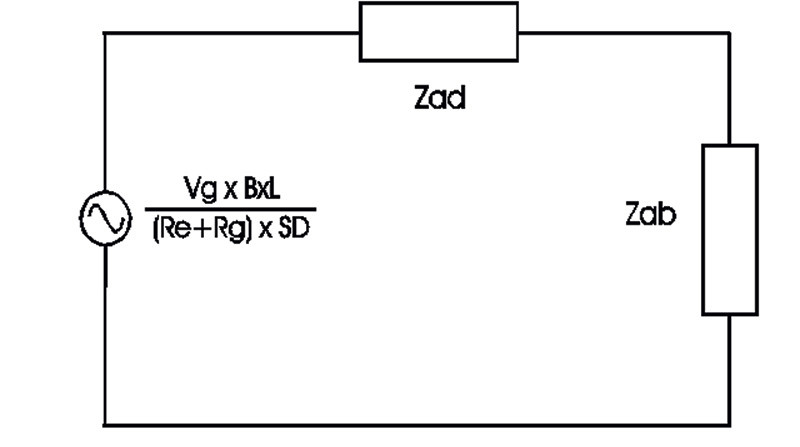
Fig. 2. Modello acustico con l’uso dei sotto-moduli.
Ho già sottolineato come all’aumentare della precisione del modello matematico aumentino di pari passo anche le domande indiscrete alle quali dobbiamo in qualche modo rispondere, domande che per altro spesso ci colgono impreparati. Se per uno studioso è relativamente facile quantificare con una buona approssimazione sia Ral che Rab, per un autocostruttore è più facile ipotizzarne le cause per quantificarne con precisione gli effetti. Ed è proprio in questa direzione che ci siamo mossi nel realizzare il modulo acustico completo della sospensione pneumatica in AFW.
Abbiamo spesso raccomandato ai nostri lettori di misurare con una certa attenzione le proprie realizzazioni, nella convinzione che si riesca ad acquisire più esperienza dalle misure di un diffusore già realizzato che da 100 pagine di letture teoriche. Per quanto riguarda le perdite e la precisa “centratura” della frequenza di accordo non ci interessa tanto rilevare in qualche modo la risposta in frequenza, tanto per non mettere in cantiere l’acquisto di strumentazione sofisticata, ma soltanto quella dell’impedenza, relativamente facile da ottenere anche con strumenti semplici, alla portata di tutti, cercando di supplire alla carenza di strumenti la conoscenza delle grandezze in gioco.
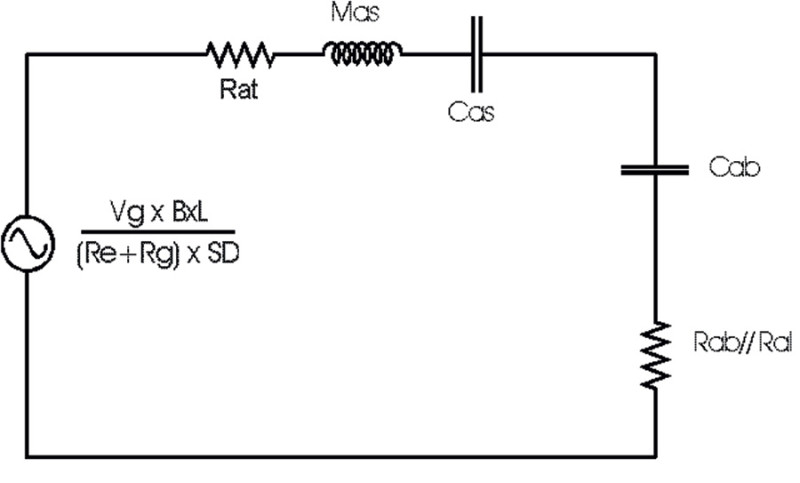
Fig. 3. Modello semplificato usato da AFW.
Sappiamo dalla teoria vista finora che risposta in frequenza e curva dell’impedenza sono strettamente correlate tra loro, costituendo semplicemente un
diverso punto di vista del sistema simulato o effettivamente realizzato. Se la curva dell’impedenza misurata su un sistema è l’esatta replica della curva simulata dal vostro software, potete esser certi che simulazione e misura della risposta in frequenza saranno identiche, mentre ovviamente piccoli scostamenti dell’impedenza porteranno a piccole variazioni della risposta acustica. Il modello matematico della sospensione pneumatica dentro AFW opera una piccola semplificazione che consente di accelerare un poco i calcoli, ma soprattutto consente di poter rispondere a domande poco impegnative, con un rovescio della medaglia assolutamente trascurabile. Si tratta in sintesi dell’eliminazione di Ral, che viene inglobata in Rab. Con questa semplificazione otteniamo il circuito equivalente di Fig. 3, ove andiamo a fare qualche considerazione. Imponendo di fatto il parallelo non consentito di Rab e Ral andiamo a compiere una operazione matematicamente scorretta, ma tenendo conto dei valori assunti da Cab per volumi che vanno da 2 a circa 500 litri con Ql e Qb variabili da 3 a 100 scopriamo che in effetti il parallelo è lecito, con le variazioni tra le due configurazioni che praticamente si distinguono soltanto sullo spessore delle linee della grafica. Questa semplificazione ci consente invece di poter sommare i due condensatori Cas e Cab in serie ottenendo Cmt e di sommare Rat e Rab in una sola resistenza che chiameremo Ratot. Ci troviamo allora ancora alle prese con un circuito risonante serie costituito, come l’altoparlante, da una resistenza, un con densatore ed una induttanza, con le stesse modalità di calcolo e le stesse formule. Cosa cambia ponendo un box totalmente chiuso alle spalle di un altoparlante? Saltando a pie pari tutte le definizioni conosciute ci baseremo soltanto sul nostro modello matematico.
Un circuito RLC serie presenta un fattore di merito dipendente dal valore dei suoi componenti secondo l’equazione:
Q = sqr(lVC)/R [1]
mentre la frequenza di risonanza è ottenibile con la formula:
Fc = 1/(2 x Pg x sqr(L x C) [2]
dove, al solito Pg è il pigreco, R è la nostra resistenza totale Ratot, L è l’induttanza Mas e C il condensatore ottenuto dalla somma in serie tra Cab e Cas. Soffermiamoci su questa ultima operazione: dalle leggi dell’elettrotecnica sappiamo che con due condensatori connessi in parallelo otteniamo un condensatore equivalente di capacità uguale alla somma delle capacità dei due condensatori, mentre sistemando come nel nostro caso due condensatori in serie otteniamo un condensatore di valore inferiore al più piccolo dei due condensatori secondo l’equazione:
Ctot = C1 x C2/(C1 + C2). [3]
Operando in questo modo otteniamo un condensatore di valore sensibilmente minore sia di Cab che di Cas, come a dire una cedevolezza minore del sistema woofer + box, un fenomeno che trova immediato riscontro nella pratica, mentre sommando in serie le due resistenze otteniamo un valore di resistenza totale maggiore di ogni singola resistenza. Forti di queste due certezze, andiamo a vedere cosa cambia nella risposta del singolo altoparlante.
Nella [2] otteniamo una diminuzione del prodotto L x C, prodotto che si trova al denominatore, motivo per il quale Fc aumenta rispetto all’originaria risonanza del woofer in aria libera. La prima certezza allora è costituita dal fatto che sistemando un box chiuso alle spalle del woofer la frequenza di risonanza del sistema aumenta di un valore dipendente dalla cedevolezza totale, modificata da quella del volume aggiunto. Il secondo effetto della diminuzione della cedevolezza derivato dall’aggiunta del volume chiuso riguarda il Q del sistema risonante. Se diminuisce C nella [1] il Q aumenta, e questo spiega il diverso andamento della risposta, che pur restando con una pendenza di 12 dB per ottava piega in maniera più decisa al diminuire della frequenza. La maggiore o minore decisione nel piegare, nel passare cioè da una risposta piatta in media frequenza ad una risposta che si attenua al diminuire della frequenza, è dovuta proprio al Q, che nel caso della cassa chiusa si chiama Qtc, mentre nel caso dell’altoparlante in aria libera si chiama Qts.
Per chiarire a cosa si va incontro scegliendo vari tipi di Q andiamo a vedere il grafico di Fig. 4, dove possiamo vedere la diversa risposta a bassa frequenza di sospensioni pneumatiche fatte risuonare tutte a 100 Hz, ma con diversi Qtc, variabili dallo smorzatissimo Qtc=0,5 al certamente poco smorzato Qtc=2.
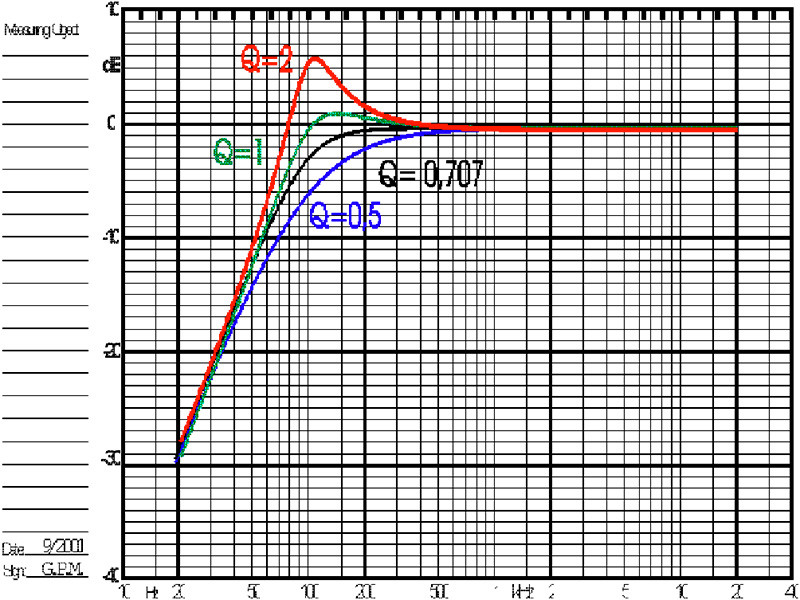
Fig. 4. Risposte al variare del Qtc.
Come possiamo vedere il Qtc =2 comporta una esaltazione alla frequenza di risonanza che vale esattamente 6,02 decibel rispetto alla banda passante, provenienti dall’equazione:
Pressione a Fc = 20 x log (Qtc).
Il progetto
Per poter disegnare un box per una sospensione pneumatica occorre la conoscenza dei tre parametri fondamentali dell’altoparlante, la frequenza di risonanza Fs, il volume equivalente Vas ed ovviamente il fattore di merito totale Qts. L’approccio al progetto viceversa può partire da varie scelte e può giungere alla massimizzazione del volume del cabinet da costruire, alla frequenza di risonanza in cassa oppure al fattore di merito del sistema, legato come sappiamo all’andamento della curva nelle vicinanze della piegatura dalla risposta lineare. Prima di definire le semplici equazioni e verificarle con qualche esempio è bene spendere due parole sulla qualità e la quantità dell’assorbente acustico. Contrariamente a quanto potrebbe sembrar lecito l’immissione di materiale assorbente in un box totalmente chiuso non diminuisce il volume a disposizione del woofer ma lo aumenta.
L’azione dell’assorbente in realtà è abbastanza complessa, sia nella quantificazione pratica che nella parametrizzazione del modello acustico. Potremmo allora decidere di evitare la presenza di tale materiale, fonte di indecisione e di poca precisione, ma sfortunatamente occorre ricordare che spesso il woofer caricato dalla sospensione pneumatica è chiamato a riprodurre anche le frequenze medie, le cui lunghezze d’onda sono paragonabili alle dimensioni del mobile. Se guardiamo al parallelepipedo di legno come ad una piccola sala d’ascolto ci possiamo immediatamente rendere conto di come nell’ambiente si possono generare interazioni, risonanze e forti localizzazioni di energia. A seconda della fase delle onde sonore all’interno del box rispetto a quelle emesse dal woofer verso l’esterno possiamo avere due fenomeni di colorazione diversa. Se le onde sonore emesse dal lato posteriore della membrana dopo aver attraversato una delle tre dimensioni del box tornano indietro in fase con quanto emesso dalla membrana stessa verso l’esterno possiamo contare su una somma, con la pressione che aumenta in quell’intervallo di frequenze, mentre se il percorso tra lato posteriore del woofer, parete del box e ritorno avviene in controfase ci troviamo di fronte ad un abbassamento repentino della risposta. Dal grafico di risposta è visibile che la presenza di materiale assorbente riesce a “smussare” facilmente picchi ed avvallamenti rallentando l’attraversamento delle onde sonore attraverso le sue fibre e dissipando sotto forma di calore parte dell’energia ricevuta. Si capisce allora come rallentando la velocità del suono la lunghezza da attraversare appaia maggiore, proprio come in un box di dimensioni maggiori. Ovviamente non è tutto oro quello che luccica e bisogna porre delle limitazioni molto forti a questo apparente vantaggio. L’azione di rallentamento dipende dalle caratteristiche costruttive del materiale assorbente, dalla sua densità, dal suo spessore ed ovviamente dalla sua quantità. Messa fuori legge la lana di vetro per la sua tendenza a polverizzarsi ed essere pericolosamente respirabile, abbiamo perso un materiale attendibile ed efficace ma abbiamo evitato un rischio sottile e pericoloso, motivo per il quale ripieghiamo volentieri su poliuretano espanso a celle aperte, su materiali similmente porosi ed sull’ormai universale pannello acrilico, simile all’ovatta ma leggermente meno denso, più lavorabile in fogli ed in ultima analisi meglio gestibile nel diffusore. L’azione di aumento fittizio dell’assorbente ci deve far distinguere allora tra volume virtuale Vab e volume fisico Vb, visto che ad un box di 100 litri può corrispondere un volume virtuale effettivamente “visto” dal woofer di oltre 130 litri, quando il box è riempito di acrilico semipressato. Comunque gli svantaggi derivanti dall’uso dell’assorbente possono essere condensati in uno soltanto, che da solo condiziona risposta, fattore di merito ed impedenza. Come abbiamo potuto vedere dal nostro modello matematico l’assorbente acustico pone in serie al volume una resistenza che di fatto limita la corrente circolante e quindi la risposta ad essa associata. Rappresenta sempre un errore teorizzare soltanto sulla variazione della velocità del suono attraverso il materiale assorbente e dimenticarsi della resistenza aggiunta in serie al sistema e la conseguente attenuazione della risposta. Ben lo sanno quegli appassionati che si affannano a costruire linee di trasmissione ben farcite di lana naturale attribuendo a questa i meriti del “basso veloce” che ad una analisi più attenta risulta essere semplicemente migliore smorzamento della curva di risposta, ovvero minore Q del sistema e quindi maggiore attenuazione all’uscita della linea.
Le “sacre formule”
Come ho detto precedentemente ci sono diversi punti di partenza e di arrivo nel progetto di una cassa a sospensione pneumatica, ma formule alla mano andiamo a vedere come tentarne una quantificazione. La prima formula ci permette di valutare il volume del box partendo dalla conoscenza del Qtc che vogliamo ottenere:
Vb = Vas/[(Qtc/Qts)2-1]
mentre la seconda ci permette di conoscere la frequenza di risonanza del sistema una volta scelto il Qtc:
Fc = Fs x Qtc/Qts.
Da queste due formule possiamo trarre utili indicazioni circa i parametri caratteristici di un woofer-tipo per la cassa chiusa. Innanzitutto balza agli occhi che un Qts leggermente più elevato della media avvicina la frequenza di risonanza in cassa chiusa a quella del woofer in aria libera e che una bassissima risonanza del woofer abbassa di fatto la risposta ottenibile in gamma bassa. Questa constatazione da sola condiziona praticamente tutta la costruzione di un woofer per sospensione pneumatica. Il Qts è inversamente proporzionale al fattore motore, per cui elevati Qts sono dovuti a fattori motori non esaltanti, cosa che va a discapito della sensibilità, così come la frequenza di risonanza molto bassa. Torna utilissima allora una cedevolezza elevata che consente bassa frequenza di risonanza con masse mobili non elevatissime ed un diametro notevole per far salire la sensibilità. Nella pratica si impiegano Qts compresi tra 0,35 e 0,55, con cedevolezze che vanno da 1 a 1,4 mm/N, ed ovviamente con equipaggi mobili dotati di escursioni generose. Da un semplice computo appare ovvio anche che per contare su sensibilità prossime agli 88-90 dB occorrano diametri che vanno dai dieci pollici in su.
Un esempio pratico
Prendiamo un altoparlante che abbia questa terna di parametri di base:
Fs = 33 Hz – Qts = 0,4 e Vas = 50 litri,
imponendo un Qtc “canonico” di 0,707, che non rappresenta sempre il meglio ma certamente offre buone garanzie di smorzamento, maggiori di qualsiasi carico reflex. Con la prima delle due formule vediamo che per tale Qtc occorrono 23.53 litri mentre con la seconda calcoliamo la frequenza di risonanza che vale 58,32 Hz. Ma c’è un ma. Questo tipo di calcolo nella pratica NON ci porta ai risultati ipotizzati in termini di Qtc, e questo per un motivo semplicissimo, non abbiamo tenuto conto delle perdite! Essendo improponibile un mobile di cemento armato di un metro di spessore con gli spigoli interni ben arrotondati è implicito che non otterremo mai un Q delle perdite dal valore elevatissimo (200). Praticamente impiegheremo un cabinet in medite da un pollice di spessore, con un incollaggio perfetto e perdite ridotte, cosi da poter contare su un Q equivalente a circa 20. In questa già invidiabile condizione possiamo
interrogare AFW e scoprire, con un certo panico, che il Qtc è sceso a circa 0,68 proprio in virtù delle pur contenute perdite indotte dal box.
Tastiera alla mano notiamo che per ripristinare l’originale 0,707 o 0,71 che dir si voglia occorre “smagrire” il box a 19,1 litri, cosa che certamente non dispiace. Se però abbiamo bisogno che il woofer emetta anche oltre i 400-500 Hz, occorre aggiungere una leggera coibentazione.
Rivestendo per esempio soltanto le pareti interne con uno strato di acrilico da 1,5 centimetri di spessore andiamo a variare nella finestra del l’assorbente sulla sinistra dello schermo le condizioni operative scegliendo la voce “assorbente alle pareti”. In questo modo possiamo da un lato rimpicciolire il volume a circa 17 litri accettando un aumento delle perdite (Fig. 5), oppure dall’altro lasciare il box a 19 litri ed “ammorbidire” il Qtc. Ipotizzando invece un riempimento totale con assorbente non particolarmente compresso abbiamo bisogno di soli 14,7 litri per il nostro Qtc. Ogni volta che alteriamo le condizioni di assorbimento AFW aggiorna il grafico di risposta, di impedenza e di MOL. Una occhiata al picco di impedenza della frequenza di risonanza chiarisce i cambiamenti. In caso di mancanza di assorbente il picco va addirittura fuori grafico valendo 32,96 ohm, mentre nella condizione di massimo riempimento vale soltanto 14,7 ohm. Rimane la scelta allora se accettare un leggero abbassamento della pressione alla risonanza con un box molto contenuto oppure avere basse perdite ed andamento ottimale della curva di risposta con un volume di dimensioni maggiori.
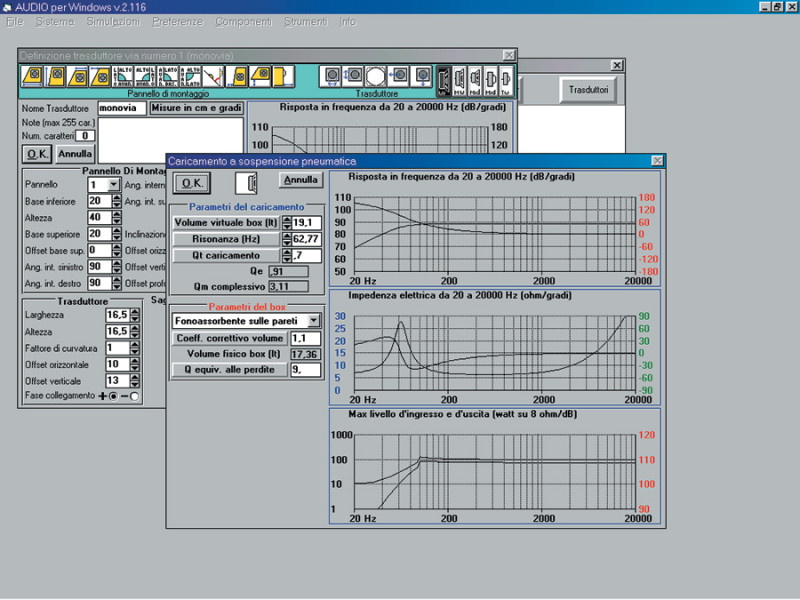
Fig. 5. Modifica dell’assorbente nella sospensione pneumatica
Ah, che bello poterlo sapere prima!
Gian Piero Matarazzo
Teoria e pratica del bass reflex
Dopo le puntate dedicate alla modellizzazione dei circuiti acustici siamo quest’oggi a parlare dei diffusori bass reflex, prima dal punto di vista concettuale e teorico e poi da quello pratico. Di cosa si tratta? Ma è semplice: prendiamo una cassa totalmente chiusa, facciamo una apertura e ci fissiamo sopra un condotto di accordo, un cilindro cavo per far passare l’aria. Bene, abbiamo costruito in pochissimo tempo un diffusore bass reflex. Sembra difficile ed invece non lo è. Peccato che tutte le equazioni appena viste per la sospensione pneumatica siano praticamente inutilizzabili! Con la solita teoria andiamo a vedere le modifiche imposte al semplice modello della sospensione pneumatica.
Come sappiamo abbiamo aggiunto una fetta di circuito a destra del volume, un circuito composto da una induttanza in serie ad una resistenza. Tutto qui, eppure il modello si complica e le scelte da fare diventano molte di più. Innanzitutto, risposte alla mano, possiamo dichiarare di essere passati da un passa-alto del secondo ordine (12 decibel per ottava) ad un passa-alto del quarto ordine (24 decibel per ottava) caratterizzato da una risposta più estesa in gamma bassa e da un andamento della fase che risulta molto peggiore. Eppure siamo di fronte alla configurazione certamente più usata a livello planetario nella costruzione dei diffusori, una scelta praticamente obbligatoria poi se il diffusore deve essere di piccole dimensioni o se deve scendere in frequenza al massimo delle sue possibilità. Andiamo allora, prima di altre considerazioni, a vedere quale sono i vantaggi di questa configurazione. Sistemando un condotto di accordo in un diffusore ed accordandolo come una canna d’organo ad una frequenza molto bassa chiamata Fb per di versificarla da Fc, requenza di risonanza della cassa chiusa, noi facciamo in modo che parte dell’energia dovuta all’emissione posteriore del woofer che nella sospensione pneumatica andava irrimediabilmente persa, venga recuperata ed emessa assieme al woofer. Tutto questo avviene soltanto alla frequenza di accordo, che scelta molto in basso si somma al contributo del woofer estendendo la risposta totale che altrimenti il woofer non sarebbe capace di emettere. A parità di volume più è bassa questa frequenza e più la risposta totale diventa smorzata, mentre se è più alta del lecito la risposta totale si gonfia con una certa enfasi e noi parliamo di sistema poco smorzato. Insomma, la frequenza di accordo sembrerebbe regolare l’andamento della risposta. Anche il volume gioca la sua buona parte di copione, visto che a parità di frequenza di accordo aumentando il volume la risposta risale mentre diminuendolo si smorza notevolmente ma perde estensione. Praticamente, gestendo volumi e frequenze di accordo possiamo estendere la risposta notevolmente più in basso, ma i vantaggi non finiscono qui, visto che dobbiamo ancora concentrarci su quello che avviene nel condotto. Questo, come abbiamo visto, prende parte della pressione generata dal lato posteriore del woofer e la porta fuori, con due caratteristiche salienti.
- La pressione emessa dal condotto è in opposizione di fase rispetto a quella emessa dal woofer.
- Lo spostamento del woofer alla frequenza di accordo si riduce fin quasi ad annullarsi ed a testimonianza di ciò la curva di impedenza elettrica mostra un vistoso abbassamento del modulo alla frequenza di accordo.
Molti sono soliti affermare che il bass reflex aumenta la sensibilità del sistema e che aumenta anche fortemente la dinamica. Niente di tutto questo ovviamente è vero e vediamo perché. La sensibilità è una caratteristica legata ai parametri elettroacustici del woofer che, per fortuna, non sono alterati dal sistema scelto per il caricamento a radiazione diretta. La maggiore dinamica è effettiva soltanto fino alla frequenza di accordo, al di sotto della quale la membrana del woofer risulta scontrollata e la sua escursione aumenta in modo vertiginoso al diminuire della frequenza, mentre nella sospensione pneumatica più in basso della frequenza di risonanza rimane più o meno costante.
Comunque il conto tra i vantaggi della maggior estensione e di una buona tenuta in potenza fino alla frequenza di accordo riescono ancora a spuntarla rispetto agli svantaggi costituiti da un volume di lavoro mediamente maggiore e da un andamento della fase acustica notevolmente peggiore.
La tecnica dietro il bass reflex
Concettualmente abbiamo già analizzato in altre occasioni alla modellizzazione del bass reflex con la teoria dei sottomoduli.
Come visibile in Figura 1 si tratta di uno schema già abbastanza semplice, che diventa semplicissimo utilizzando i sotto moduli di Figura 2, la cui quantificazione tiene conto delle perdite, del volume di lavoro ed ovviamente delle dimensioni fisiche del condotto di accordo. Un altro mito che va sfatato è quello del calcolo della frequenza di accordo che risuona soltanto col volume a disposizione e NON col woofer, tanto che in un box di 30 litri accordato con un condotto a 40 Hz non c’è variazione alcuna sia se il woofer montato è da un pollice o da dieci pollici.

Figur 1 – Il modello matematico completo del bass reflex con tutte le sue perdite.

Figura 2 – Il modello enormemente semplificato con l’uso dei sottomoduli.
Cambia la risposta ottenuta, certo, ma la frequenza di accordo non si muove nemmeno di un Hertz. Questo perché nella formula per il calcolo delle dimensioni del condotto si tiene conto soltanto del volume con cui il condotto deve risuonare e la frequenza alla quale ciò deve avvenire, senza scomodare alcun parametro caratteristico dell’altoparlante impiegato.
Ma prima di spiegare come dimensionare il condotto andiamo a vedere come calcolarci il volume e la frequenza di accordo per ottenere un buon bass reflex.
Come affermato dal nostro Direttore Tecnico la prima quantificazione seria, basata su calcoli matematici autorevoli, venne da Neville Thiele che la pubblicò in Australia, suo paese di nascita, senza ricevere una grande attenzione da parte degli addetti al lavori. Solo successivamente un suo al lievo Richard H.
Small ripubblicò lo studio sul giornale dell’AES in America, aggiungendo allo studio di Thiele il computo delle perdite per un modello certamente più realistico e terreno. Il successo fu enorme e molti altri studiosi iniziarono ad avvicinarsi a questa configurazione, che in breve tempo soppiantò definitivamente la sospensione pneumatica. Lo studio di Thiele e quello successivo di Small avevano come fine ultimo quello di usare la solita terna di parametri caratteristici dell’altoparlante (Fs, Vas e Qts) per una quantificazione precisa del miglior tipo di accordo. I primi nove accordi della tavola di Thiele e delle tabelle di Small definivano i tipi di accordo in base all’analogia con i filtri passa-alto del quarto ordine.
Partendo dall’accordo 1 si passava da andamenti simili ad un quasi Butterworth del terzo ordine fino ad un filtro di Butterworth del quarto ordine, contraddistinto con il numero 5, oltre il quale si passava ad un andamento della risposta simile ai Chebychev, caratterizzati da un certo ripple, e decisamente mal smorzati.
Dall’accordo N. 1 si parte col Qts più basso preso in considerazione, che vale 0,18, mentre nell’accordo più alto, il N. 9, si prende in considerazione il massimo Qts ammesso (0,557), che di fatto stabilisce un valore da non superare. In questa tavola e nelle successive tabelle di Small il tipo di accordo da scegliere rimaneva però ancorato al valore del Qts, al quale poteva essere abbinato un solo tipo di andamento della risposta. Solo qualche anno dopo D.B. Keele aggirò brillantemente l’ostacolo con una ricerca che approdò al metodo del “compliance shift”, uno slittamento virtuale della cedevolezza che permetteva di ingannare i calcoli e consentiva la quantificazione di uno qualunque degli accordi di Thiele a partire da un Qts qualsiasi, purché non troppo lontano da quello ideale. Si immetteva in effetti un coefficiente di errore Cn, ottenuto dal rapporto tra Qts ideale per quel tipo di accordo ed il Qts dell’altoparlante a disposizione elevati al quadrato. Questo scarto di cedevolezza poteva assumere qualunque valore compreso tra 0,25 e 4, proprio il metodo impiegato da AFW per suggerire volumi e frequenze di accordo in base all’allinea mento di Thiele. Oggi per fortuna non c’è bisogno di fare calcoli molto sofisticati e complessi, visto che nel programma di AR basta imporre un accordo qualunque e visualizzare immediatamente il risultato al lato in meno di un battito di ciglia… Le due formule che comunque permettono un andamento identico al Butterworth del quarto ordine (detto anche B4) e che definiscono frequenza di accordo e volume di carico sono le seguenti:
Fb = F3 = 0,39 x Fs / Qts e Vb = 6,27 x QtsA2 x Vas.
Va notato infatti che la frequenza a -3 decibel di un sistema B4 coincide con la frequenza di accordo. Con queste equazioni qualunque woofer il cui Qts parte da 0,2 ed arriva fino a circa 0,45 può essere accordato in reflex con un andamento della risposta simile al B4. Una seconda coppia di equazioni, più benevola nei confronti del volume di carico pur permettendo un accordo massimamente piatto, è la seguente:
Fb = Fs x 0,4185 /Qts, F3 = Fs x 0,443/Qts
e Vb =4,33 x Qts2 x Vas.
Come è possibile vedere, Fb ed F3 sono leggermente diverse, mentre il volume risparmiato è notevole, a tutto vantaggio dello smorzamento e della tenuta in potenza.
Una volta definito il volume e la frequenza di accordo abbiamo tutti gli elementi per calcolare le dimensioni di accordo.
Contrariamente a quanto potrebbe sembrare a prima vista maggiore è il diametro del condotto e maggiore è la lunghezza che questo deve avere per potersi accordare correttamente al volume che ci interessa. Non bisogna disegnare condotti molto lunghi perché questi potrebbero risuonare “in proprio” a quarto d’onda, proprio come una canna d’organo. Dall’altro lato non si possono realizzare condotti troppo piccoli perché quando la velocità dell’aria che passa attraverso il condotto aumenta eccessivamente fino a superare l’otto per cento della velocità del suono (circa 27,5 metri al secondo equivalenti a 99 km/h) il flusso diventa disordinato ed il condotto tende “a soffiare”, come si dice in gergo, ed a farlo in maniera fastidiosamente udibile. La dimensione minima del diametro oltre la quale non si può scendere, per condotti a sezione costante, è dovuta ad una formula che lo stesso Small dichiara essere fortemente empirica:
Dmin = 0,56 x D x SQR (Xmax)/SQR(SQR(Fb))
dove Dmin rappresenta il diametro del condotto espresso in millimetri, D quello del woofer, sempre espresso in millimetri, così come Xmax, che è la massima escursione del cono. Fb rappresenta la frequenza di accordo espressa in Hertz e l’operazione SQR, al solito, rappresenta la radice quadrata. Stabilito questo diametro, siamo pronti a calcolare la lunghezza del condotto con l’ultima formula:
L = [c2/(16x Pg) x d2/(Vb x Fb2)]-(0,85 x d)
dove e rappresenta la velocità del suono (344 m/s) Pg è il pi greco (3,1415…) d è il diametro del condotto espresso in millimetri Fb è la frequenza di accordo espressa in Hz.
Audio For Windows consente anche l’allineamento B6 con filtro elettronico, un escamotage dovuto a Newman, un altro studioso d’oltre oceano. In pratica, visto che alla frequenza di accorcio il woofer è praticamente fermo, si può inserire un circuito attivo in preamplificazione che esalta di circa 6 decibel la risposta alla frequenza di accordo senza quasi alterare l’escursione del woofer. A questo punto, è possibile scendere notevolmente con la frequenza di accordo di un valore pari alla radice quadra di 2 e “centrare” questa frequenza col filtro elettronico riallineandone la risposta. Newman suggeriva di partire da un accordo B4 spostando la Fb dal valore originario ad un valore:
Fb nuovo = Fb orig : 0,707
e di realizzare un passa-alto elettronico del secondo ordine con fattore di merito 2 centrato alla nuova frequenza di accordo. Un utile sottoprodotto di questa circuitazione è costituito dal fatto che limitando la risposta al di sotto della frequenza di accordo col filtro elettronico si riduce di fatto anche l’escursione, che come sappiamo nei reflex è priva di controllo. In pratica possiamo estendere il concetto ed affermare che con qualunque tipo di accordo è possibile estendere la risposta verso il basso spostando la Fb più in basso, dimensionando un filtro elettronico alla stessa frequenza e variando il Q del filtro fino a “raddrizzare” la curva di risposta totale.
AFW anche in questo caso torna preziosissimo, perché consente di vedere in tempo reale come varia la risposta operando variazioni al filtro elettronico. Per piccoli volumi accordati a frequenze molto basse può però succedere che le dimensioni minime di un condotto diventino improponibili in relazione alle dimensioni del box. In questi casi si fa ricorso a condotti a sezione non costante, che hanno il pregio di diminuire drasticamente l’innesco di soffi dovuti alla velocità dell’aria. I profili utilizzati vanno dall’apertura conica del condotto alle forme esponenziali ed a forma di clessidra, sostanzialmente simili nel funzionamento ma profondamente diverse nella realizzazione pratica. Il calcolo comunque rimane molto complesso e ripetitivo. Questa annosa faccenda che ben conoscono gli appassionati più smanettoni può essere aggirato andandosi a leggere l’articolo “Teoria e pratica del condotto di accordo” pubblicato sul n. 104 della consorella ACS AudioCarStereo, ove si esplorano tutti i casi possibili, e poi scaricando successivamente i due programmi illustrati in quell’articolo disponibili gratuitamente sul nostro sito. Buon lavoro!
Gian Piero Matarazzo
tratto da AUDIOreview n. 219 dicembre 2001