Un mio amico, fisico sperimentale, è solito affermare che quello che non si può misurare non esiste. Questa affermazione, certamente non applicabile a concetti astratti come l’amore, l’odio, la fedeltà e il tradimento, è certamente vera in ambito scientifico. Anche i più sofisticati argomenti di fisica teorica (ora va di moda il campo di Higgs) restano appunto teorici fino a che gli esperimenti non li confermano o li smentiscono ed è valsa la pena di spendere miliardi e miliardi per le apparecchiature (il Large Hadron Collider) atte a verificare la questione.
Da decine di anni il laboratorio di AUDIOreview è all’avanguardia nello sperimentare nuove tecniche di misura per indagare la realtà fisica che sta dietro all’ascolto musicale. È stato quindi con piacere che ho accolto l’invito di Fabrizio Montanucci a collaborare con il team di AR per indagare la struttura più intima del DSD, prima da un punto di vista teorico, poi sperimentale e infine corroborando il tutto con ascolti sistematici. In questa coppia di articoli analizziamo il problema del rumore, per poi occuparci in seguito della risposta in frequenza.
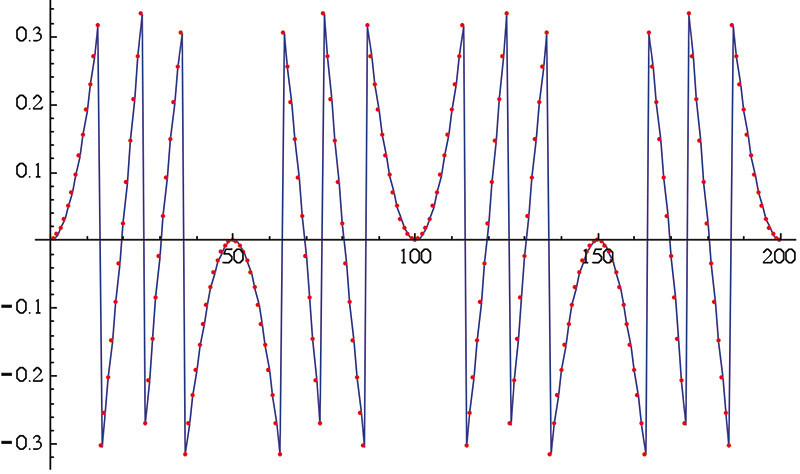
Figura 1. Errore di quantizzazione per un campionamento a 2 bit di un segnale sinusoidale con 100 punti per periodo; i punti dell’errore sono stati uniti per evidenziarne la regolarità dell’andamento.
Il Rumore di Quantizzazione
Il Teorema del Campionamento garantisce che un segnale infinito, di larghezza di banda limitata, campionato per tutta la sua durata infinita (producendo quindi una quantità infinita di numeri reali a precisione infinita) può essere ricostruito esattamente utilizzando una combinazione lineare dei suoi infiniti campioni con funzioni di lunghezza infinita. Questo è chiaramente solo un risultato teorico di Analisi Matematica, ogni applicazione pratica deve prevedere una durata finita del segnale e una rappresentazione dei numeri con precisione finita; esistono infinite diverse approssimazioni di questo tipo e questo fa sì che non si può parlare di suono di un segnale digitale, quello che suona è il segnale analogico dopo una conversione digitale/ analogica e ai fini della qualità non si può non tenere conto di questa seconda fase.

Figura 2. Spettro del rumore di quantizzazione (in blu) per un segnale multitono (in rosso); (a) senza dither, (b) con dither (in blu).
Il processo in cui a un numero reale (con campo di variazione continuo) si sostituisce un numero intero, che assume un numero discreto di valori, è detto Quantizzazione e l’errore risultante è detto Rumore di Quantizzazione. Per poter valutare la bontà del processo di quantizzazione è necessario studiare con cura l’errore che si commette approssimando il segnale continuo con quello discreto. Si tratta di un’analisi delicata che comporta la discussione di sottili questioni matematiche.
La prima considerazione da fare è che l’errore di quantizzazione è una quantità puramente matematica come il segnale digitale stesso.
La seconda considerazione è che da un punto di vista matematico qualunque tipo di deterioramento del segnale può essere visto come rumore additivo; si preferisce fare però la distinzione tra rumore e distorsione considerando il primo come il risultato di un processo stocastico scorrelato con il segnale di partenza (per esempio il rumore termico) mentre la seconda è il risultato di un fenomeno correlato con il segnale di partenza (per esempio la distorsione di intermodulazione).
Nel caso dell’errore di quantizzazione si possono verificare entrambe le situazioni; per esempio, se si discretizza una sinusoide l’errore è fortemente correlato con il segnale.
Nel caso che il segnale d’ingresso sia sinusoidale e di ampiezza massima, si ottiene la ben nota equazione per il rapporto segnale-rumore espresso in dB:
SNR ≈ 6,02 n + 1,76 (1)
Che per n=16 (il valore scelto per i CD audio) risulta un SNR di circa 98 dB.
Questa formula, che spesso viene applicata sistematicamente in modo ingenuo, impone invece alcune considerazioni:
- Il termine 6,02 n mostra che per ogni bit in più nella parola di quantizzazione si guadagnano circa 6 dB di rapporto segnale-rumore. Non si deve però credere che n possa essere aumentato a piacere in quanto ogni apparecchiatura realizzata fisicamente ha dei limiti invalicabili legati al rumore termico.
- Il termine 1,76 è legato al fatto che si è considerato un segnale di ingresso sinusoidale; in genere un segnale musicale reale, a parità di valore massimo, ha una potenza molto minore e si possono perdere anche più di 10 dB di rapporto segnale-rumore.
- Tutta l’analisi viene fatta supponendo che il massimo livello del segnale sia esattamente l’accettazione limite. In pratica, poiché quando l’accettazione limite viene superata si verifica una inaccettabile distorsione, viene sempre lasciato un margine di tolleranza di qualche decibel che va anch’esso a scapito del rapporto segnale-rumore.
- In ogni caso anche se il massimo livello del segnale fosse esattamente l’accettazione limite, un segnale musicale ha in genere momenti in cui il livello è elevato e altri in cui questo è anche molto basso (i fortissimi e i pianissimi delle esecuzioni sinfoniche) e nei pianissimi il rapporto segnale-rumore può essere molto sfavorevole.
ATTENZIONE: le problematiche ai punti 2, 3 e 4 valgono anche per l’audio analogico.
Potenza di Rumore e Spettro di Rumore, il Dither
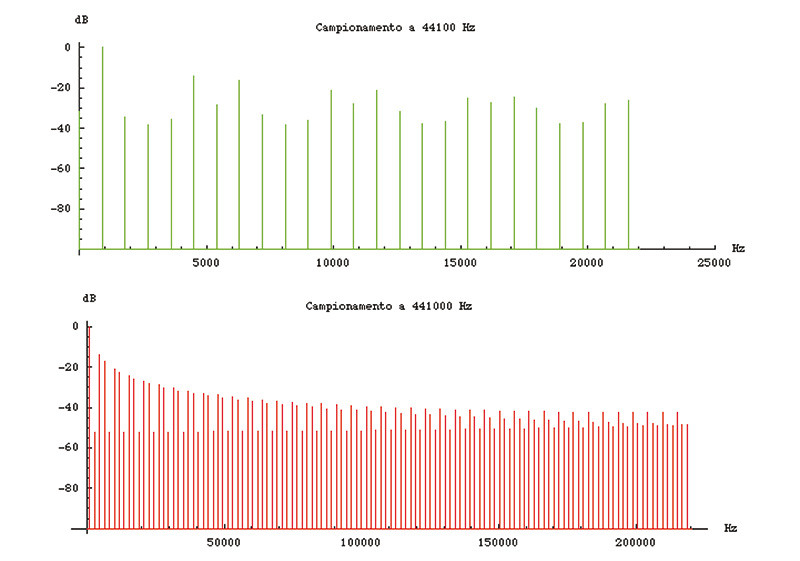
Figura 3. Spettro di un segnale sinusoidale a 1.000 Hz campionato ad un bit per due diverse frequenze di campionamento.
La formula (1) fornisce la potenza totale di rumore su tutta la banda riproducibile, ma non dice nulla su come tale rumore sia distribuito tra le varie frequenze; tipicamente l’errore di quantizzazione è correlato al segnale come ben si vede provando a quantizzare un segnale multitono (ovvero la somma di tante sinusoidi a 0 dB e con frequenze equidistanti tra loro).
Se si paragona la banda audio ad un sentiero su cui si debba camminare scalzi, il rumore correlato si presenta come dei pezzi di vetro piantati in verticale (fanno molto male). Decorrelare il rumore equivale a frantumare i pezzi di vetro distribuendoli uniformemente su tutta la larghezza del sentiero. Esiste una tecnica di facile applicazione che permette di fare ciò: se si aggiunge al segnale da campionare un rumore stocastico di piccolo valore questo fa sì che l’errore di quantizzazione diventi anch’esso un rumore con buone proprietà statistiche, pagando un leggero aumento della potenza totale di rumore
Si possono aggiungere al segnale da quantizzare dei valori estratti a sorte in modo uniforme (rectangular dither); facendo le scelte giuste, il rapporto segnale/rumore peggiora di 3 dB ma la media dell’errore di quantizzazione viene forzata a zero. Un’altra possibilità è di aggiungere al segnale da quantizzare la somma di due dei valori estratti a sorte in modo uniforme (triangular dither); in questo caso il rapporto segnale peggiora di 4,8 dB, la media dell’errore di quantizzazione viene forzata a zero e la varianza assume un valore costante.
Alcuni autori ritengono che il rumore inevitabile nel segnale di partenza (rumore termico, fruscio del nastro, del LP, ecc.) possa fungere da dither rendendo accettabile l’errore di quantizzazione anche in assenza di un dither artificiale.
Relazioni tra rumore e frequenza di campionamento
Notiamo che, anche se il segnale da rappresentare è stato filtrato passa-basso prima della digitalizzazione, lo spettro della funzione quantizzata non può essere limitato in frequenza perché gli errori non lo sono. Quindi, per il teorema del Campionamento, queste componenti ad alta frequenza vengono ribattute sotto la frequenza di Nyquist sotto forma di aliasing. Passando nel dominio della frequenza si riesce a vedere bene come stanno le cose. Se facciamo una rappresentazione di un segnale quantizzato ad un bit dopo un campionamento a 44.100 Hz e a 441.000 Hz (esempi puramente didattici) nel primo caso il rumore viene spalmato solo in banda audio mentre nel secondo è distribuito fino a 220.500 Hz; in questo secondo esempio è anche visivamente evidente come lo spettro del rumore venga ribattuto alla frequenza di Nyquist.
Se il rumore di quantizzazione ha un buon comportamento (per esempio si può assimilare al rumore bianco) allora la distribuzione conseguente all’aumento della frequenza di campionamento causa una diminuzione della potenza di rumore in banda audio. In pratica ogni raddoppio della frequenza di campionamento causa una riduzione di 3 dB della potenza di rumore in banda audio. In altre parole se si allarga il sentiero, la quantità totale di vetro (la potenza di rumore) resta la stessa ma la sua altezza dove si cammina (spettro del rumore in banda audio) diminuisce.
Sigma Delta e Noise Shaping
Ognuno di noi, davanti al sentiero pieno di vetri, prima di camminarci scalzo ci darebbe una bella spazzata. Se il sentiero è largo (ovvero se la frequenza di campionamento è molto grande) è un’operazione facile, e per questo è subito entrata nella prassi audio con il nome generico di Noise Shaping (rimodellamento del rumore). Si possono distinguere tre campi di applicazione:
- conversione analogico/digitale;
- conversione digitale/analogico;
- riquantizzazione, ovvero diminuzione della lunghezza della parola.
Prendiamo in considerazione il terzo caso, più semplice da trattare e da sperimentare con il computer. Supponiamo di avere un segnale con frequenza di campionamento molto maggiore di 20 kHz e lunghezza di parola di 24 bit e vogliamo ridurre la parola a 10 bit (per esempio per pilotare un amplificatore PWM) o addirittura ad 1 bit (per ottenere un segnale DSD); l’idea consiste nel calcolare l’errore commesso ad ogni passo di riquantizzazione (i bit persi) e usarlo, opportunamente filtrato, per correggere il segnale in entrata al riquantizzatore. Questo procedimento è molto efficace alle basse frequenze ma aumenta l’errore alle alte frequenze; in altre parole toglie i vetri da dove si deve camminare (banda audio) e li ammucchia a lato.
A seconda della topologia si parla di tecnica Sigma Delta, se il filtro è sul percorso del segnale, o di Noise Shaping vero e proprio, se il filtro è sull’anello di reazione del segnale (Figura 4). Le due topologie sono equivalenti se F(z) = H(z)/(H(z) + 1) ma nei casi (1) conversione DA e (2) conversione AD è più semplice usare la tecnica Sigma Delta, ormai adottata nella stragrande maggioranza dei convertitori integrati.
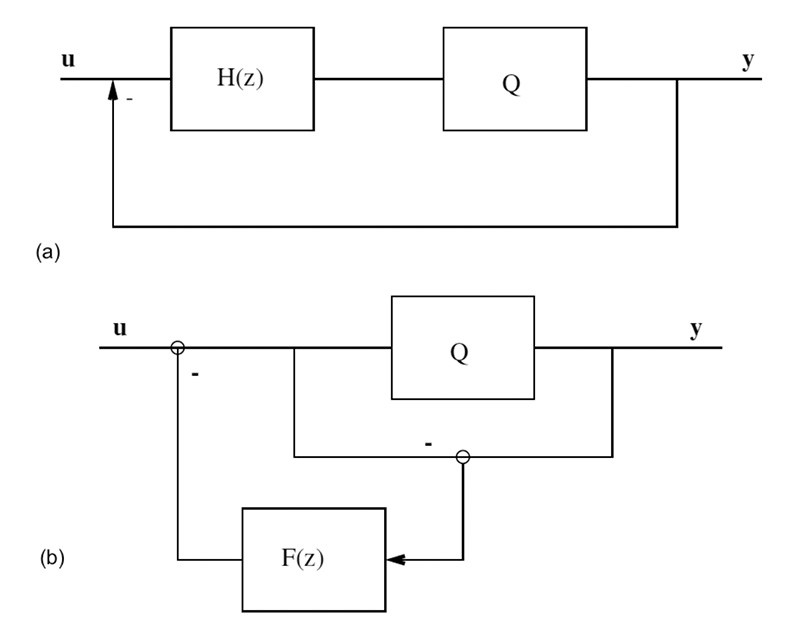
Figura 4. Configurazioni Sigma Delta (a) e Noise Shaping (b); u è il segnale in ingresso, y quello in uscita e Q rappresenta il (ri)quantizzatore. Se H(z) e F(z) hanno valori opportuni, i due processi sono equivalenti.
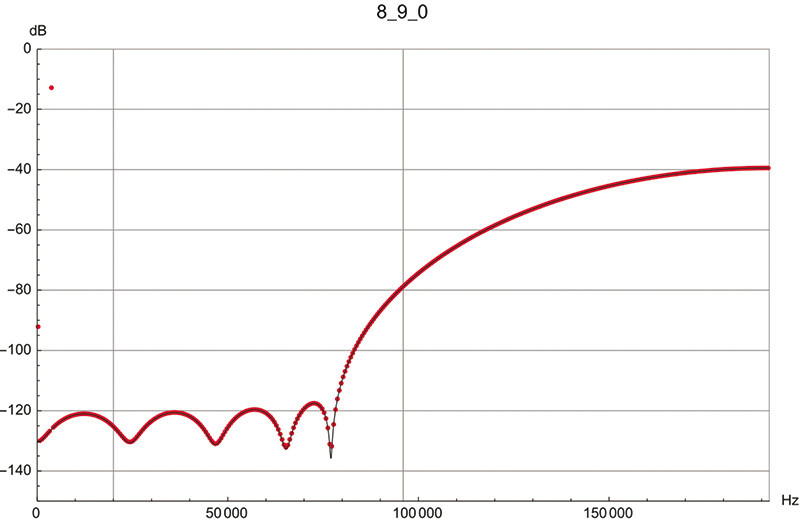
La funzione F(z) viene realizzata con un filtro FIR e i suoi valori determinano la curva di rimodellamento del rumore. La Figura 5 mostra un esempio simulato da me con un filtro a 9 coefficienti con banda utile di 80 kHz in un passaggio da 24 a 10 bit.
Progettare il filtro FIR, da cui dipende la bontà dell’operazione di rimodellamento, è un compito delicato perché bisogna diminuire il rumore udibile mentre contemporaneamente aumenta la quantità del rumore totale; è necessario un compromesso, e la scelta migliore può essere verificata solo all’ascolto. Un altro problema notevole è assicurare la stabilità del sistema; non esistono risultati teorici, in genere nel passaggio al DSD si ottengono sistemi stabili per un segnale fino al 50% della modulazione massima. È interessante il fatto che a differenza del PCM nel DSD il clipping può essere reso dolce, più o meno come negli amplificatori valvolari.
È fondamentale sottolineare ancora come dal punto di vista matematico il segnale DSD non sia altro che un’onda quadra che oscilla tra i valori 1 e -1, e questo significa che la sua potenza ha un valore costante di +3 dB rispetto alla sinusoide al clipping che viene usata come riferimento per lo 0 dB. Considerando che il segnale buono ha sempre una potenza molto più bassa, tutto il resto è rumore e l’uso del Noise Shaping non è un abbellimento opzionale ma una parte fondamentale del processo di conversione.
Finiamo la trattazione teorica affrontando il problema più cattivo. Abbiamo già detto che vi sono infiniti modi per associare un segnale continuo ai campioni PCM, e ciò vale anche nel caso del DSD in cui non è univocamente definito né il metodo per creare il segnale DSD, né il metodo per convertirlo in analogico e neppure un metodo per confrontare la qualità di un segnale DSD con l’equivalente PCM. In [2, 6], un segnale DSD e un segnale PCM sono definiti equivalenti se danno gli stessi valori nei punti del campionamento PCM se trattati con un filtro continuo passa-basso. Ai puristi che, a questo punto, diranno che il digitale è un gran casino e che è meglio restare nell’analogico, facciamo notare come vi siano anche infiniti modi per fare un giradischi o un violino. Il nostro punto di vista è che spesso l’applicazione di una tecnica molto complessa, specie se fatta con passione, diviene un’arte.
Nelle pagine che seguono Fabrizio espone i risultati delle nostre sperimentazioni, io mi limito ad aggiungere che tutte le volte che ciò era tecnicamente possibile i miei calcoli e i risultati del laboratorio di AUDIOreview hanno concordato perfettamente, confermando la validità dell’approccio.
di Francesco Romani
Bibliografia
[1] A. Allegri, M. Benedetti, DSD vs PCM, AUDIOreview, 352, pp. 78-82, giugno 2014
[2] D. Birru, Use of comb filters for efficient VLSI implementation of reduced clock frequency noise shapers, Electronics Letters, 32 (4), 1996
[3] F. Montanucci, Le misure sui DAC-DSD, AUDIOreview, 351, pp. 75-80, maggio 2014
[4] D. Reefman, E. Janssen, Signal processing for Direct Stream Digital, Philips, 2002.
[5] F. Romani, Il DSD suona meglio del PCM?, AUDIOreview, 357, pp. 28-31, novembre 2014
[6] E. Roza, Recursive Bitstream Conversion: the Reverse Mode, IEEE Transactions On Circuits And Systems-11: Analog And Digital Signal Processing, 41 (5), 1994








Mi sono spesso chiesto se il lavoro fatto da AudioReview e dai suoi collaboratori fosse facile o no. Un mio amico, violinista concertista e insegnante (in fuga, da anni, all’estero), prima dell’affermazione delle tecnologie digitali in campo sonoro era solito proporsi da purista nei confronti delle evoluzioni tecnologiche e concettuali degli strumenti musicali e delle modalità di ascolto della musica. Era purista al pari di chi propende per lo strumento analogico rifiutando a priori un approccio matematico basato sulla natura e la misura di suono e rumore: a chi prefigurava punti di vista differenti in merito alle possibilità di “suonare” solo con strumenti tradizionali obiettava che, per un orecchio sufficientemente allenato, certamente a tale differenza di approccio sarebbe corrisposta una “tara” di qualità e di espressione certamente individuabile. Nei primissimi anni ’90 ebbi modo di prendermi una rivincita con l’ascolto di un CD (di Nigel Kennedy, che al tempo non disdegnava ne’ il repertorio classico ne’ la tecnologia, mentre ora sembra esser sotto abiura dell’una e dell’altra cosa): “Suona davvero bene” mi disse, laconico, l’amico violinista. Sarà stato probabilmente anche merito del (non più che accettabile) lettore Denon, che probabilmente lavorava per dare conferma anche auditiva a quanto matematicamente atteso. Non voglio con ciò però affermare o equivocare il fatto che il mezzo (o il costo) per l’ascolto possa giustificare, garantire e dimostrare un buon ascolto. D’altronde anche io ho qualche malizioso amico fisico teorico che lascia intendere come gli stati intermedi delle particelle osservate nell’LHC possano essere interpretati anche come stati definitivi se è necessario giustificare i costi del progetto. In definitiva credo sia sempre lecito diffidare di preconcetti e pregiudizi: a maggior ragione è inaccettabile ogni pregiudizio verso i responsi della matematica nell’audio digitale. E temo che invece il concetto di rumore e ascolto sia comunemente alimentato dall’incuria nella scelta della propria dotazione di strumenti d’ascolto base o in altre parole (e per quello che potrebbe apparire un eccesso di piaggeria) dalla mancata consultazione degli articoli tematici (su AudioReview, of course!). Il timore sembra aggravarsi nei casi in cui il concetto di ascolto è limitato a contenuti sonori talmente privi di dinamica e talmente compressi sulla gamma media, per i quali sembra arduo far emergere valori idonei alle misure di qualità di cui si parlava. Fate un lavoro davvero difficile, sapete?
Un saluto,
Cordialmente.
T.C.