Teoria e pratica dei filtri digitali – parte 2

Nonostante i primi studi sui filtri digitali risalgano alla fine degli anni ’40 e, con la diffusione dell’audio
digitale, il loro impiego sia ormai largamente diffuso anche in ambiente domestico, il loro principio di
funzionamento è scarsamente noto al di fuori dell’ambito specialistico. Questa serie di articoli si propone di
introdurre all’attenzione degli appassionati e dei professionisti i principali aspetti teorici e applicativi connessi
con l’impiego e l’utilizzazione nell’audio dei filtri digitali.

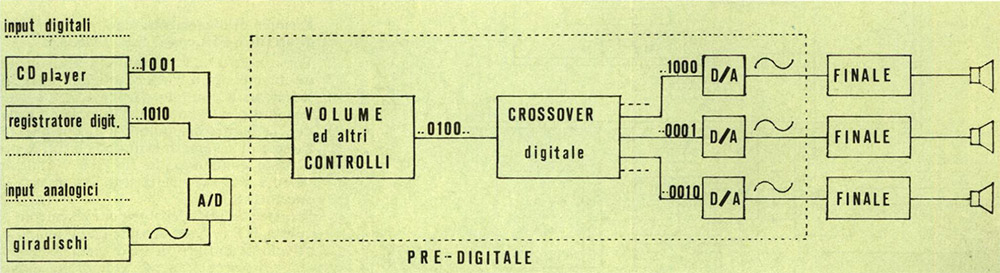
Sul numero 51 di AUDIOreview è stata presentata in anteprima la prova del compact disc player Philips CD 650, che presenta alcune fondamentali novità rispetto ai modelli attualmente in commercio. Tra queste, la presenza dell’uscita digitale è l’innovazione che più di ogni altra ci fa intravedere quale sarà l’ormai prossimo futuro dell’alta fedeltà. Infatti, l’impianto hi-fi «tipo» sarà composto da una sorgente digitale, quale il CD player o il registratore digitale, da un preamplificatore digitale, da un crossover digitale, dai finali di potenza e naturalmente da una coppia di diffusori acustici. Il segnale, prelevato dall’uscita digitale della sorgente, viene inviato attraverso un unico filo (trasmissione delle informazioni di tipo seriale) ad uno degli ingressi del pre-digitale.

Occorre a questo punto ricordare che il segnale presente all’uscita digitale del CD player non contiene soltanto informazioni di tipo «musicali», cioè non è la pura e semplice conversione digitale del segnale musicale analogico originale, ma contiene anche una grande quantità di informazioni ausiliarie che servono per la sincronizzazione, per l’inibizione della copia, eccetera.

Tutto quanto riguarda la struttura del «protocollo» usato per trasferire i segnali digitali audio si può trovare in «L’uscita digitale» (AUDIOreview n. 51). Lo schema a blocchi del sistema hi-fi del futuro è mostrato in fig. 1.

Come è stato già accennato nella prima parte di «Teoria e pratica dei filtri digitali, (AUDIOreview n. 51), il blocco che costituisce la parte fondamentale di ogni apparecchiatura audio digitale è il filtro digitale. In quell’articolo si era cercato di chiarire cos’è, a cosa serve e come funziona teorica mente un filtro digitale. Ci occuperemo ora della sua implementazione, entrando più in dettaglio sul suo funzionamento pratico.

Implementazione di un filtro digitale

Nella prima parte di «Teoria e pratica dei filtri digitali» avevamo per prima cosa chiarito il seguente concetto: poiché i segnali di ingresso e d’uscita di un filtro digitale non sono altro che numeri binari (a 16 bit nello standard hi-fi), il funzionamento di un tale dispositivo deve essere necessariamente basato su un opportuno algoritmo di calcolo.

In altre parole, il segnale da filtrare (sia esso proveniente da un compact disc o da un processo di conversione analogico-digitale) viene sottoposto ad un certo numero di operazioni aritmetiche prima di poter essere inviato all’uscita del filtro. Tali operazioni possono essere solamente di tre specie: somma, moltiplicazione e ritardo di un campione. Tra i vari tipi di filtri digitali che si possono implementare combinando opportunamente le tre suddette operazioni la nostra attenzione si è accentrata sui filtri FIR (finite impulse response) con risposta all’impulso simmetrica, poiché essi godono della importante proprietà di avere una risposta in fase costante qualunque sia la loro risposta in ampiezza.

Lo schema di funzionamento di un filtro FIR con quattro coefficienti è mostrato in fig. 2. Esaminando tale schema possiamo ricavare l’espressione che ci da il campione di uscita Y (n) corrispondente al campione d’ingresso X (n):
1) Y (n) = h0*X (n) + h1*X (n-1) + h2*X(n-2) + h3*X(n-3)

Più in generale, se avessimo m celle di ritardo di un solo campione (blocchi ^Z-1), tale espressione diventerebbe:
2) Y (n) = hO*X (n) + hl*X (n-1) + hm*X (n-m)

dove occorre ricordare che i coefficienti hi non sono altro che i campioni della sequenza risposta alla sequenza impulso unitario, e che quindi la risposta in frequenza di un filtro FIR dipende esclusivamente da loro.

Tale risposta in frequenza ha la forma:

dove il modulo di H rappresenta la risposta in ampiezza mentre l’argomento rappresenta la risposta in fase del filtro.

Ricordiamo che la risposta di un filtro digitale sarà tanto migliore (in termini di pendenza di attenuazione e di ripple) quanto più elevato sarà il numero m di coefficienti del filtro. Potremmo a questo punto pensare di «costruire» praticamente un filtro digitale utilizzando un certo numero di unità aritmetiche e logiche separate (sommatoli, moltiplicatori, registri) connesse tra loro su di un’unica piastra secondo lo schema topologico del filtro in esame. Nel caso del semplice filtro a tre.celle di ritardo di fig. 2 questo tipo di approccio potrebbe risultare una soluzione, in termini di economia e di ingombro, ancora attuabile. Con l’aumentare della complessità del filtro, cioè all’aumentare del numero di coefficienti, tale soluzione diventerebbe irrealizzabile per dei sistemi audio digitali. Ad esempio, per implementare il solo filtro FIR a 120 coefficienti presente all’interno di un chip del già menzionato Philips CD 650 occorrerebbe una piastra molto più grande dell’intero CD player. Sistemi digitali di questo tipo vengono oggi usati solamente per applicazioni molto particolari, come ad esempio nei sistemi RADAR, dove il costo e l’ingombro hanno un’importanza relativa rispetto alla elevatissima velocità di calcolo che tali sistemi possono raggiungere.

Il D.S.P.

A questo punto sembrerebbe che l’unica soluzione «ragionevole» per implementare dei filtri numerici per audio digitale sia quella di utilizzare un microprocessore programmato «ad hoc» per effettuare tutte le operazioni di calcolo necessarie per la realizzazione di un filtro digitale. In questo caso ci troveremmo però di fronte ad una difficoltà insuperabile, costituita dalla insufficiente velocità di calcolo di un normale microprocessore.

Infatti, come sappiamo, nello standard dell’hi-fi digitale domestica la frequenza di campionamento è pari a 44.100 Hz, vale cioè a dire che tra un campione ed il successivo trascorre un intervallo di tempo pari a soli 22,6 microsecondi. Per avere quindi una elaborazione «in tempo reale» (presupposto indispensabile nell’audio digitale) si devono eseguire tutte le operazioni di calcolo, che vanno ripetute per ogni campione d’ingresso X (n), in un tempo inferiore a 22,6 microsecondi.

Analizziamo ora quali possibilità avrebbe un moderno microprocessore a 16 bit (quale ad esempio il 68000 della Motorola) di compiere tutte le operazioni aritmetiche richieste nel calcolo di un filtro FIR. L’operazione critica in tutti i microprocessori è la moltiplicazione: ad esempio il 68000 effettua una moltiplicazione 16 x 16 bit in circa 10 microsecondi, ed una somma in circa 2 microsecondi (naturalmente questi valori dipendono anche dal clock usato). Ne consegue che per calcolare ad esempio un filtro FIR a 10 coefficienti (e quindi di prestazioni abbastanza modeste) occorrerebbe un tempo totale di circa 120 microsecondi, largamente superiore al tempo di calcolo che abbiamo a disposizione nell’hi-fi digitale.

Le esigenze di velocità di calcolo, di economia, di ingombro, imprescindibili nelle applicazioni di alta fedeltà, hanno spostato l’interesse dei progettisti verso una nuova generazione di microprocessori, i cosiddetti D.S.P. (Digital Signal Processor). Tali D.S.P. presentano molte affinità con i comuni microprocessori, come ad esempio la programmabilità e la versatilità, ma posseggono rispetto a questi delle caratteristiche di velocità estremamente superiori.

Al momento attuale, il D.S.P. costituisce il giusto compromesso tra compattezza dell’hardware, velocità di elaborazione, programmabilità e costo nelle realizzazioni di sistemi per i processi digitali dei segnali.

Esempio di implementazione di un filtro FIR con D.S.P. TMS 320

Tra i molti D.S.P. disponibili attualmente in commercio, il TMS 320 della Texas Instruments è risultato particolarmente interessante per le buone caratteristiche generali, la buona disponibilità di documentazione e di sistemi di sviluppo ed infine per il costo contenuto. In fig. 3 è visibile lo schema a blocchi della struttura interna di questo D.S.P.

Per dare un’idea della velocità di calcolo di questo D.S.P. basti pensare che il tempo di calcolo di un filtro FIR è di circa 400 nano secondi per coefficiente. Quindi per implementare un filtro FIR a 10 coefficienti come quello dell’esempio precedente occorrerebbero solamente circa 4 microsecondi (cioè un tempo 30 volte inferiore a quello necessario al 68000).

Da un esame della struttura interna del TMS 320 osserviamo che è presente, tra gli altri componenti, una RAM («DATA RAM») di 144 locazioni di memoria di 16 bit ciascuna.

Supponiamo ora di implementare un filtro FIR a 4 coefficienti e descriviamo l’evolversi del calcolo «step by step». Scegliamo 9 locazioni della DATA RAM suddivise come in figura 4.

Nell’assegnazione delle locazioni è indispensabile, per una corretta ed efficiente implementazione, disporre le locazioni relative ai campioni att iali e ritardati (X0, X1, X2, X3) in modo consecutivo, con il campione attuale nella locazione più bassa ed in senso crescente le locazioni dei ritardi successivi. Si può facilmente intuire che il numero di locazioni necessarie di RAM interna per un FIR ad m coefficienti sono 2 x m + 1 (m locazioni per i campioni d’ingresso X (i) che vengono man mano «sniffati» verso l’alto, m locazioni per i coefficienti ed infine una locazione per il campione d’uscita Y). Essendo quindi 144 il numero di locazioni di memoria della DATA RAM ne consegue che è teoricamente possibile implementare un filtro FIR con un massimo di 71 coefficienti; è indispensabile però verificare se il tempo di calcolo che tale filtro comporta rientra nel periodo di campionamento.

Torniamo al nostro esempio, e supponiamo che i campioni provenienti da una campionatura in tempo reale o da una memoria di massa (come il CD) vengano acquisiti nella locazione X0. Inizialmente si suppone anche che le altre locazioni siano state azzerate. Per ogni campione acquisito andranno eseguite 4 moltiplicazioni tra i coefficienti hi ed i relativi campioni presenti nelle locazioni Xi ed i risultati, accumulati in Y, forniranno il campione d’uscita.

Nella fig. 5 è illustrata la struttura hardware interna al D.S.P. relativa all’operazione di moltiplicazione. Il prodotto tra due numeri avviene caricando il moltiplicando (cioè il campione presente nella locazione Xi) nel registro T con l’istruzione:

LT Xi

Successivamente si esegue l’istruzione di moltiplicazione per il coefficiente hi:

MPY hi

A questo punto, dopo l’istruzione MPY (tra due parole a 16 bit ciascuna) il prodotto si trova nel registro P a 32 bit e può essere spostato, sommato o sottratto all’accumulatore A con le istruzioni PAC, APAC e SPAC.

In figura 6 è mostrata la struttura del programma relativa a questo esempio. Una particolare attenzione merita la descrizione dell’istruzione LTD, in quanto essa mette in rilievo l’elevata capacità di parallelismo di questo processore. Tale istruzione permette, con un solo ciclo, di:

a) caricare il registro T con il moltiplicando Xi;
b) shiftare Xi nella locazione Xi +1 (cioè esegue l’operazione Z);
c) sommare all’accumulatore A il risultato del prodotto precedente.

L’accumulazione, in A, dei prodotti su 32 bit, viene troncata a 16 bit prima di essere immagazzinata nella posizione di RAM Y.

Controlliamo il tempo di esecuzione del nostro filtro, ricordando che il TMS 320 ha una velocità di calcolo di circa 200 nanosecondi per ciclo. L’istruzioni IN e OUT richiedono 2 cicli ciascuna, tutte le altre 1 ciclo. Abbiamo quindi 15 cicli di 200 nanosecondi ciascuno, per un totale di 3 microsecondi (quindi un tale filtro potrebbe lavorare ad una frequenza di campionamento di circa 330.000 Hz, molto superiore a quella dello standard hi-fi). Riferendosi ai dati ottenuti nello sviluppo del programma, notiamo che il calcolo di una «tappa» FIR (formata dalle istruzioni LTD e MPY) richiede, come già accennato in precedenza, 0.4 microsecondi. Chiediamoci ora qual è il numero massimo di tappe che il nostro D.S.P. potrebbe calcolare alla frequenza di campionamento in uso nello standard dell’hi-fi digitale domestica, cioè 44.100 Hz: facendo dei semplici calcoli ci accorgiamo che si potrebbe riuscire al massimo ad implementare un filtro FIR di 53 «tappe».

A questo punto il programma relativo al calcolo del filtro FIR potrebbe essere immagazzinato in memorie non volatili secondo le due possibilità illustrate in fig. 7a) e 7b).

Nella prima il programma è fissato nella memoria esterna di programma (fino a 8 Kbyte), nel secondo caso lo stesso programma viene  immagazzinato dal costruttore, con un processo di mascheratura, nella memoria interna di 3 Kbyte. Il secondo caso, «chip mascherato», costituisce un esempio di come un D.S.P. per impieghi generali possa essere dedicato permanentemente a svolgere una particolare funzione.

Nel nostro caso il chip D.S.P. diventerebbe un filtro digitale FIR con caratteristiche prefissate.

In una fase di sviluppo è però necessario poter provare, e all’occorrenza modificare il software, nonché avere la possibilità di generare tale software in grado di interfacciarsi, da un lato con l’utente e dall’altro con il D.S.P. Proprio per tale scopo esistono «sistemi di sviluppo» commerciali, interfacciabili con diversi computer. In particolare la piastra mostrata nella foto di pag. 55 in AUDIOreview n. 51, possiede un’interfaccia con IBM PC che consente di effettuare queste operazioni in maniera efficiente e con un costo estremamente contenuto. Lo schema del suddetto sistema completo è mostrato in fig. 8.

In questo caso il software sviluppato su IBM PC, una volta portato alla forma di codice oggetto, viene trasferito nella memoria di programma del D.S.P. (memoria RAM) e risulta quindi controllabile a turno dal PC o dal 320. Infatti, una volta caricato in memoria il programma (in tale fase siamo ancora sotto il controllo del PC), si fa in modo che il controllo passi al D.S.P., il quale continuerà a poter scambiare informazioni nei due sensi con il PC attraverso le porte di INPUTOUTPUT.

Conclusioni

Nel primo articolo della serie dedicata ai filtri digitali avevamo visto come il funzionamento di tali dispositivi fosse basato su degli algoritmi di calcolo costruiti adoperando tre sole operazioni: somma, moltiplicazione e ritardo di un campione. Nel secondo, cioè in questo stesso articolo, abbiamo cercato di chiarire in che modo si possono eseguire praticamente tali operazioni con una velocità tale da rimanere nell’ambito dell’elaborazione in tempo reale.

Nella prossima puntata, avvalendoci delle considerazioni fatte fino ad ora, vedremo come si possa progettare e realizzare praticamente un crossover digitale, e analizzeremo i risultati da noi ottenuti con il nostro prototipo funzionante.

 

di Lindoro Massimo del Duca – Roberto Lucchesi – Rosaria Ferrarese

da AUDIOreview n.53 settembre 1986