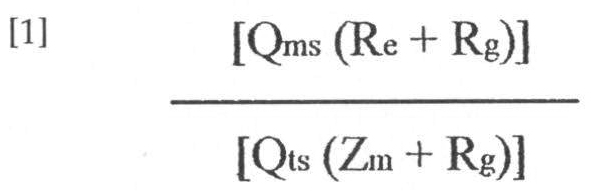Misteri e meraviglie del pilotaggio in pura corrente
(seconda parte)
Nel corso della prima parte abbiamo esaminato quali siano i vantaggi dell’operare in corrente anziché in tensione quando si pilota un altoparlante dinamico, ed abbiamo illustrato inoltre una tecnica di «recupero» dello smorzamento elettrico perduto attuata mediante un particolare filtro attenua banda.
In questa puntata esaminiamo quella che secondo noi è la tecnica ottimale per attuare il pilotaggio in corrente, sia ai fini dello sfruttamento ottimale dei componenti sia in termini di semplicità e ridotta criticità della parte elettronica.
Come vedremo, quest’ultima può al limite addirittura essere più semplice di quella necessaria per realizzare un convenzionale allineamento reflex B6.
di Fabrizio Montanucci
Allineamenti elettromeccanici in pura corrente
Se ad un autocostruttore qualunque chiediamo cosa succede se, ad un altoparlante pilotato da una sorgente di tensione ideale, mettiamo in serie una resistenza, la risposta sarà immediata e priva di incertezze: «lo smorzamento elettrico diminuisce e quindi aumenta il fattore di merito totale, secondo il coefficiente
laddove
Rg = resistenza aggiunta in serie al generatore
Qms = fattore di merito meccanico (in aria libera)
Qts = fattore di merito totale con impedenza sorgente nulla (in aria libera)
Re = resistenza della bobina mobile
Zm = modulo impedenza alla risonanza»
In altri termini, e prescindendo dal calo complessivo di livello che si ha serializzando al trasduttore una resistenza reale, la funzione di trasferimento dell’altoparlante (in aria libera od in cassa chiusa) rimane descrivibile da un polinomio di ordine 2, in cui l’unico termine che muta è il moltiplicatore del termine di primo ordine, ovvero lo smorzamento. C’è poi un’altra relazione altrettanto nota ed importante per il prosieguo dei nostri ragionamenti, ed è quella che lega il fattore di merito meccanico in cassa (Qmb) al rapporto tra la frequenza di risonanza in cassa (Fb) e quella in aria (Fs), ovvero
[2] Qmb = Qms Fb/Fs
valida per un box ideale (privo di perdite). Vedremo, quando applicheremo la teoria ora esposta ad un progetto reale, come modificare tale relazione in un box reale.
Chiediamoci ora cosa succederebbe se la resistenza salisse a valori molto elevati (almeno un ordine di grandezza sopra l’impedenza alla risonanza), ovvero se la sorgente fosse un generatore di corrente anziché uno di tensione. La prima relazione è chiarissima: il Qt verrebbe incrementato di un fattore limite pari a Qms/Qts, rapporto che per inciso è pari a Zm/Re. Il significato fisio di tale effetto, che in termini qualitativi significa il completo annullamento dello smorzamento elettrico (l’effetto frenante offerto all’equipaggio mobile dall’essere la bobina immersa in un campo magnetico e chiusa sulla resistenza del generatore), è altrettanto chiaro, se solo si considera che in un caricamento in cassa chiusa il massimo d’impedenza corrisponde alla frequenza di taglio acustica del sistema e che il Q corrisponde al guadagno lineare alla frequenza di taglio: il pilotaggio in corrente comporta un aumento del fattore di merito della risposta acustica di un fattore pari al rapporto tra l’impedenza alla risonanza e la Re.

Tabella 1 : frequenza di taglio normalizzata e fattore di merito (degli stadi di FI ordine) dei singoli stadi costituenti filtri passa-alto di Bessel-Thomson, per ordini totali da 3 a 10.

Tabella 2: frequenza di taglio normalizzata e fattore di merito (degli stadi di II ordine) dei singoli stadi costituenti filtri passa-alto di Butterworth, per ordini totali da 3 a 10
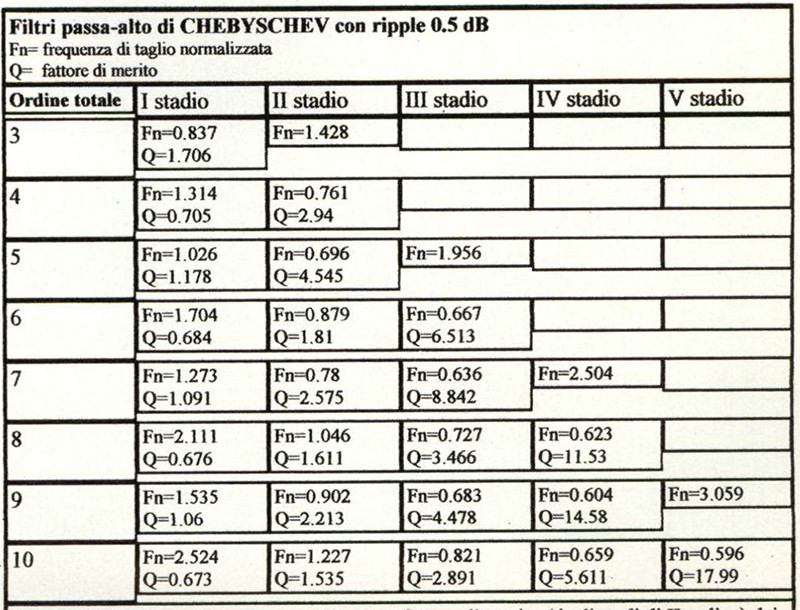
Tabella 3: frequenza di taglio normalizzata e fattore di merito (degli stadi di U ordine) dei singoli stadi costituenti filtri passa-alto di Chebyschev con ripple 0 5 dB per ordini totali la 3 a 10
A questo punto, l’autocostruttore di cui sopra si domanderà probabilmente «d’accordo, so come varia la risposta con il pilotaggio in corrente, ma visti i Qts ed i rapporti tipici Qms/Qts dei trasduttori in commmercio mi ritroverò sempre Q complessivi oscillanti tra 1 e 7/8, quando non addirittura superiori, ovvero con enfasi alla risonanza comprese tra 3 ed oltre 15 decibel. Cosa ci faccio con una risposta così irregolare e risonante?». Risposta: e se realizzassimo allineamenti elettromeccanici a sospensione pneumatica di ordine superiore al secondo, in cui l’altoparlante rappresenta solo uno degli stadi filtranti passa-alto di secondo ordine? Se diamo un’occhiata alla tabelle 1/2/3 noteremo come, in tutti gli allineamenti, al salire dell’ordine, sale il fattore di merito massimo assunto dagli stadi di secondo ordine. Inoltre, passando dagli allineamenti a più alta coerenza temporale (i Bessel-Thomson) a quelli meno smorzati (i Butterworth e soprattutto i Chebyschev) il fattore di merito massimo pure continua a salire a parità di ordine. Riguardo poi i Chebyschev, che sono gli allineamenti più «duttili» di tutti perché in essi possiamo decidere non solo l’ordine ma anche il fattore di ripple, possiamo osservare come al salire di quest’ultimo parametro salga anche il fattore di merito massimo. Abbiamo quindi immediatamente a disposizione una serie di opzioni progettuali per realizzare il nostro sistema pilotato in corrente, in ognuna delle quali dovremo operare a priori delle scelte che poi determineranno il resto del sistema. In particolare potremo fissare:
- L’allineamento e l’ordine: in questo caso dovremo torvare un altoparlante adatto a raggiungere un fattore di merito meccanico in cassa pari al più alto fattore di merito che compare nella funzione descrittiva dell’allineamento (in prima istanza, il Qms di tale altoparlante dovrà essere non inferiore a tale valore), poi dovremo diminuire il volume di carico per far salire il Qmb fino al valore desiderato. L’estensione ottenuta verso l’estremo basso corrisponderà con ottima approssimazione alla risonanza.
- L’allineamento e l’altoparlante: in tal caso dovremo fissare approssimativamente il volume di carico (e quindi la frequenza di risonanza ed il Qmb) e poi salire con l’ordine fino ad ottenere un Q massimo superiore a quello dell’altoparlante in cassa. A questo punto dovremo diminuire un po’ il volume (ovvero far salire il Q e la risonanza) fino a far coincidere il Qmb dell’altoparlante montato in cassa con il suddetto Q massimo dell’allineamento in quel particolare ordine.
- L’altoparlante e l’ordine massimo: in questo caso dovremo modulare il volume di carico (ovvero, e ci si scusi la ripetizione ma è bene essere chiari, la Fb ed il Qmb) e poi trovare quale allineamento possiamo realizzare. Se il Qmb così raggiunto sarà minore od uguale a quello di un Buterworth o meglio ancora di un Bessel, potremo ritoccare il volume fino a far coincidere tali valori, altrimenti dovremo optare per un Chebyschev e modulare il ripple fino a far salire il Q massimo al Qmb ottenuto.
- L’altoparlante ed il fattore di ripple: se decidiamo ad esempio che una certa estensione ed una adeguata dinamica possiamo ottenerle solo con l’altoparlante X montato nel volume Y, ma il Qmb così ottenuto è troppo alto per essere inserito in un allineamento di massima coerenza temporale o di massima linearità ancora fisicamente realizzabile (leggi: di ordine sufficientemente basso), potremo fissare un ripple tollerabile e cercare l’ordine più basso dell’allineamento Chebyschev che richiede uno stadio dal Q pari a quel Qmb.
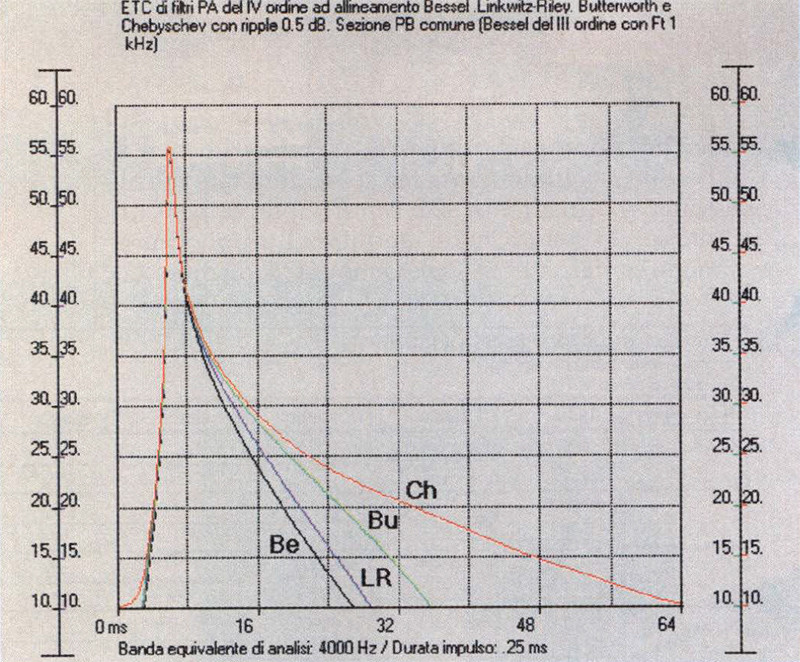
Figura 1: ETC (Energy-Time Curve) calcolate con WinCross di altrettanti filtri passa-alto di quarto ordine con F, 50 Hz. Allineamenti di Bessel (curva nera), Linkwitz-Riley (curva blu), Butterworth
(curva verde), Chebyschev con ripple 0.5 dB (curva rossa).
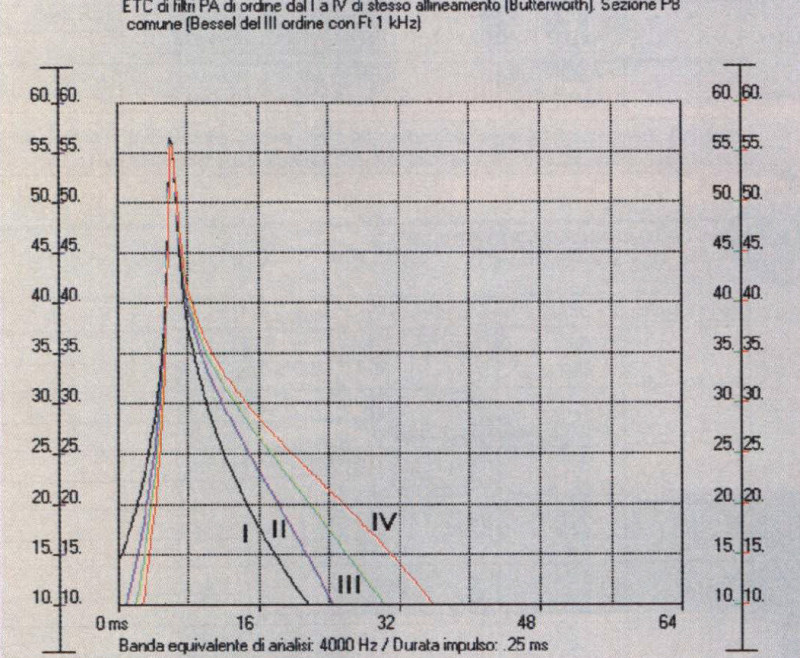
Figura 2: ETC di filtri passa-alto di Butterworth con F, 50 Hz. Primo ordine (curva ne ra), secondo ordine (curva blu), terzo ordine (curva verde), quarto ordine (curva rossa).
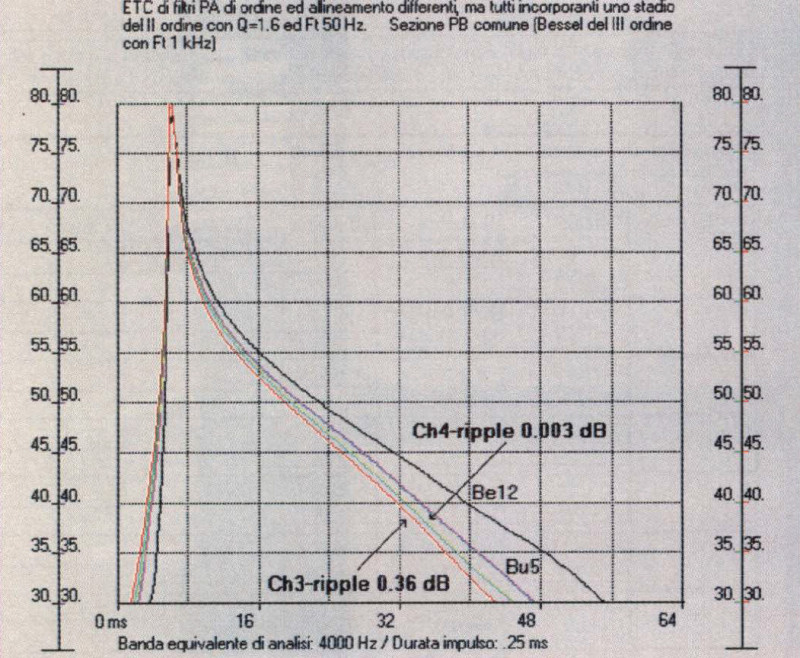
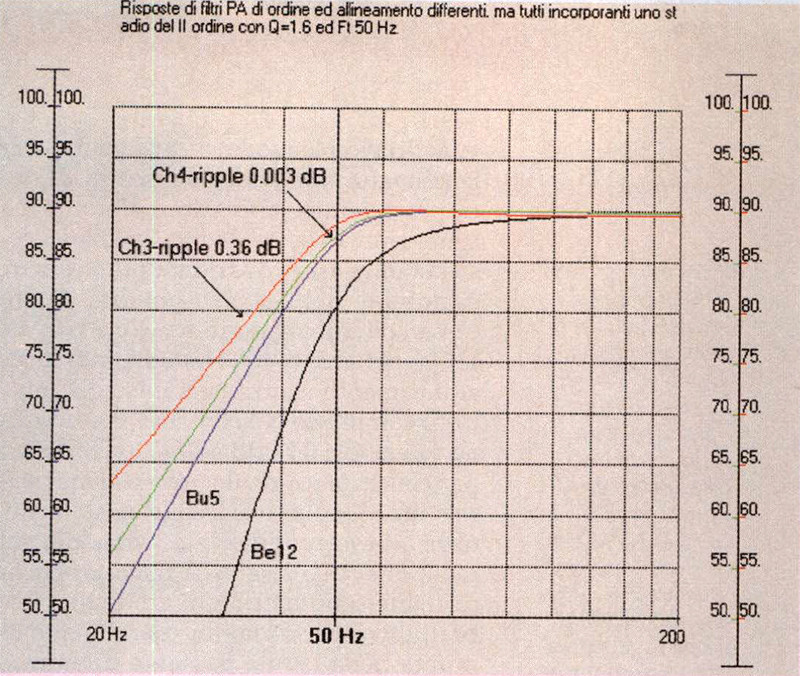
Figura 3: ETC di 4 filtri passa-alto completamente differenti, ma aventi in comune uno stadio di secondo ordine con F, 50 Hz e Q pari a 1.6 (rappresentante un ipotetico woofer in cassa chiusa pilotato in corrente). Bessel del dodicesi mo ordine (curva nera), Butterworth del quinto ordine (curva blu), Che byschev del quarto ordine con ripple 0.003 dB (curva verde), Chebyschev del terzo ordine con ripple 0.36 dB (curva rossa).
Fissato in questi termini, il problema di come realizzare un corretto allineamento elettromeccanico con il pilotaggio in corrente potrebbe apparire astruso e difficilmente districabile, ma non è affatto così, e poiché spesso un’oncia di pratica vale più di dieci libbre di teoria abbiamo approntato un box descrittivo delle fasi di sviluppo di un progetto concreto. A prescindere comunque dall’angolazione specifica rispetto alla quale si sceglie di risolvere il problema del corretto allineamento di un altoparlante pilotato in corrente, è bene comunque sottolineare a questo punto due importanti elementi progettuali:
- Per qualunque altoparlante può essere trovato un corretto allineamento elettromeccanico con cui attuare il pilotaggio in corrente.
- Qualunque allineamento elettromeccanico venga attuato, sussiste la pratica certezza che esso soddisfi il requisito di attenuazione delle frequenze inferiori a quella di risonanza in cassa, che come abbiamo visto nella precedente puntata vengono distorte maggiormente con il pilotaggio in corrente che non con il convenzionale pilotaggio in tensione. La pendenza di crescita della distorsione è infatti, al massimo, di pochi dB per ottava, ed un solo polo elettrico (ovvero un allineamento del III ordine complessivo, il minimo ipotizzabile per un sistema pilotato in corrente) basta ad attenuare le frequenze inferiori alla Fb più di quanto sarebbe necessario per mantenere invariata la distorsione armonica (al prezzo ovviamente di una maggiore pendenza in banda di transizione).
Allineamenti elettromeccanici ottimali: una nuova costante universale?
Ci si potrebbe chiedere a questo punto in che modo dobbiamo decidere di allineare il nostro bel sistema pneumatico pilotato in corrente, visto che di gradi di libertà ne abbiamo parecchi. Una volta scelto ad esempio l’altoparlante e l’estensione di banda che intendiamo ottenere, ovvero modulando la Fb attraverso il volume di carico, otterremo un certo fattore di merito della funzione di trasferimento acustica di secondo ordine. A questo punto potremo «sostituire» tale stadio di secondo ordine a quello di più alto Q di un certo allineamento. Supponiamo di avere ottenuto un Qmb pari a 1.6, che è già decisamente basso: se volessimo realizzare un Bessel dovremmo salire molto con l’ordine, addirittura fino al dodicesimo, poiché solo con tale complessità gli allineamenti di Bes- sei richiedono uno stadio di II ordine con fattore di merito pari a 1.59 (ed una Fn di 1.17); lasciamo ai lettori più sadici di immaginare quale grado di precisione dei componenti occorre per implementare decentemente il filtro elettronico di ordine 10 necessario ad un allineamento elettromeccanico siffatto!
Se ci «accontentiamo» di un Butterworth, l’ordine totale scende subito in modo drastico: già il quinto ordine richiede uno stadio con Q pari a 1.618 (ed Fn pari ad 1, come in tutti gli stadi costituenti un Butterworth), sicché basterà diminuire di poco il volume di carico (e far salire di poco la Fb) per raggiungere il Qmb ottima le e poi realizzare un filtro elettronico del III ordine che implementi la parte elettronica dell’allineamento. Se infine optiamo per un Chebyschev abbiamo a disposi zione due ordini ancora più bassi, di differente ripple: il terzo (ripple 0.36 dB) ed il quarto (appena 0.003 dB di ripple), il primo dei quali richiede un filtro elettronico solo del primo ordine e quindi ancora più semplice di quello necessario ad un classico reflex B6 (tra l’altro potrebbe essere implementato con una banalissima rete RC precedente il finale a transconduttanza).
Ma di tutti questi possibili allineamenti, quale dovremmo preferire?
Tutti i tecnoaudiofili sanno bene (e chi fosse a digiuno di tali nozioni può ad esempio tornare ad AR 155, pagg. 110/111) che gli allineamenti temporalmente più «pronti», ovvero la cui risposta impulsiva si smorza prima, sono quelli di Bessel, seguiti dai Linkwitz-Riley, dai Butterworth e dai Chebyschev, con questi ultimi sempre meno smorzati quanto maggiore è il ripple. Tutto ciò può essere visto con grande evidenza nelle 4 curve di fig. 1, ove compaiono le ETC (Energy-Time Curve) calcolate con WinCross di altrettanti filtri passa-alto ad allineamenti differenti, ma di pari ordine. Ma è anche «vox audiofili» che tanto più alto è l’ordine di un allineamento, tanto maggiore sarà il tempo impiegato dal sistema a «spegnersi» cessata l’eccitazione. Ed anche in questo caso possiamo trovare una conferma nelle 4 ETC di fig. 2, relative a 4 passa-alto di stesso allinea mento (Butterworth) ed Ft, ma di ordine crescente dal primo al quarto.
Sorge quindi un dubbio amletico: in termini di smorzamento ottenibile, è meglio un allineamento ad alta coerenza temporale di alto ordine oppure un allineamento meno coerente ma di ordine basso?
La risposta è nelle ETC di fig. 3, dove il suddetto stadio del secondo ordine (con una Ft di 50 Hz) è stato inserito in un Bessel del dodicesimo ordine (curva nera), in un Butterworth del quinto (curva blu), in un Chebyschev del quarto con ripple 0.003 dB (curva verde) ed infine in un Chebyschev del terzo ordine con ripple 0.36 dB (curva rossa). Come si vede, nonostante le «mostruose» differenze strutturali ed implementative, le curve di decadimento energetico sono inaspettatamente vicine tra loro. Inoltre i risultati migliori, pur di poco, sono ottenibili proprio con i bistrattatissimi Chebyschev, il cui basso ordine prevale sulla superiore coerenza intrinseca di Butterworth e Bessel. Ne deriva una constatazione importante: la curva di decadimento temporale di un sistema pilotato in corrente non è sostanzialmente modificabile, ovvero lo smorzamento complessivo dipende quasi esclusivamente dal valore del Q meccanico (Qmb) che si ottiene caricando l’altoparlante in un particolare volume.
E poiché anche con Qmb relativamente elevati (dell’ordine di alcune unità) è possibile allestire allineamenti di Chebyschev con ripple praticamente inudibili(frazioni di decibel) già con il quarto e terzo ordine, ne consegue che di norma non conviene salire al di sopra di questi, anche per non complicare troppo (e rendere di conseguenza eccessivamente critica) la parte elettronica.
La risposta all’impulso e la ETC
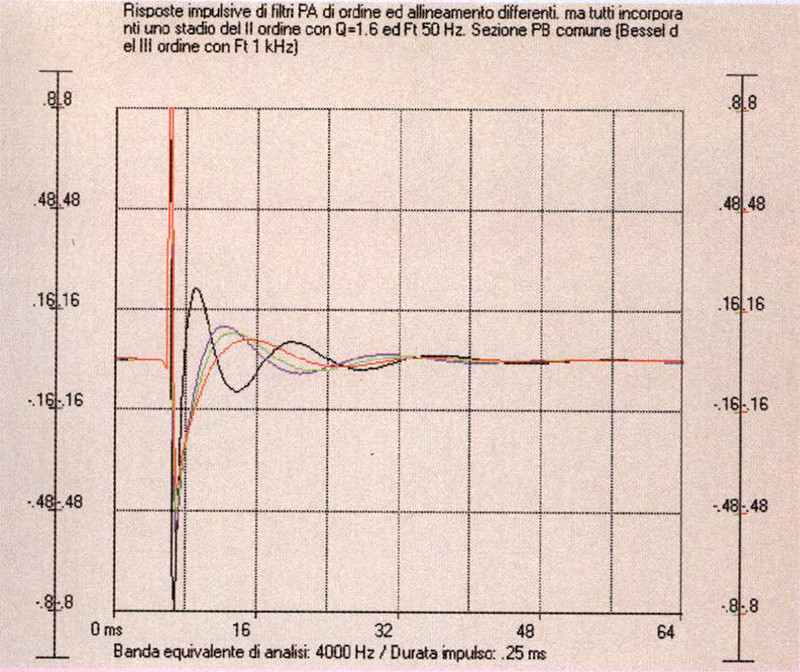
Qualcuno potrebbe chiedersi perché per quantificare lo smorzamento ottenibile con un certo allineamento filtrante abbiamo usato la ETC anziché, come apparirebbe naturale e talvolta si osserva in varie pubblicazioni, la semplice risposta impulsiva. La risposta è in fig. 5, ove compaiono gli andamenti nel tempo (l’impulso reale) corrispondenti ai filtri di fig. 3: i tracciati, pur «apparendo» simili in termini di decadimento, non sono facilmente confrontabili tra loro, perché le frequenze di ringing e la collocazione dei massimi sono alquanto differenti. Le curve tempo-energia mirano invece, valutando anche la risposta impulsiva immaginaria (che pure possiamo visualizzare con WinCross), ad esprimere non il semplice dato di pressione nel tempo, ma la somma dell’energia cinetica e potenziale posseduta dal sistema oscillante rappresentato dal trasduttore. Il termine «mirano» non lo abbiamo utilizzato a caso: già nel 1990 John Vanderkooy e Stanley Lipshitz mostrarono infatti come «… dobbiamo accontentarci di guardare alla ETC come ad un utile modo unipolare di vedere la risposta all’impulso, senza aspettarci che essa ci dia informazioni riguardo al flusso dell’energia».
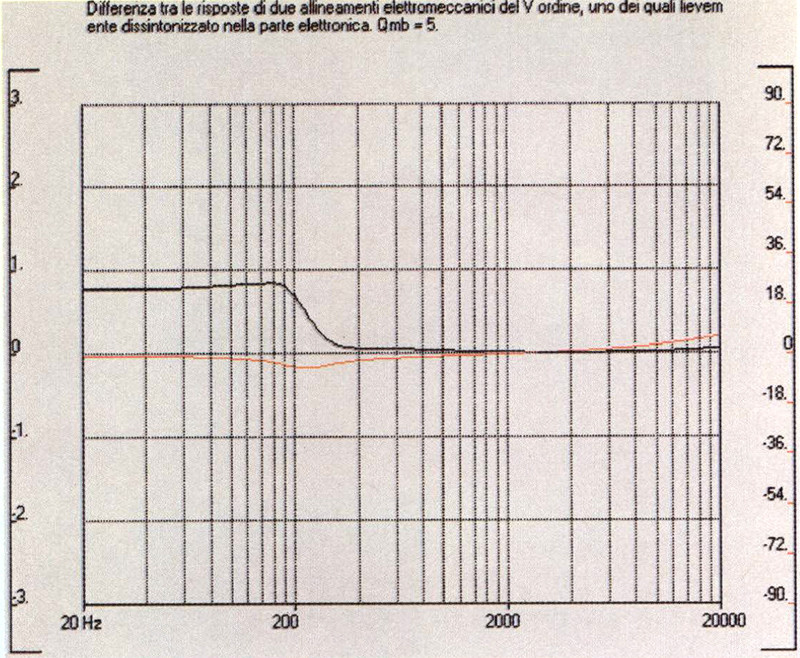
Figura 6: Differenza tra la risposta acustica di un altoparlante con Qmb=5 ed F,=150 correttamente
inserito in un allineamento di Chebyschev del V ordine (ripple 0.71 ed Ft 220 Hz) e lo stesso altoparlante pilotato con una sezione elettronica avente F, superiore del 3% rispetto a quella necessaria.
Gli altoparlanti più adatti per il «current drive»
Se è vero che qualunque altoparlante dinamico può essere vantaggiosamente pilotato in corrente secondo la tecnica che abbiamo descritto, appare subito evidente che però alcuni saranno più versati di altri. Poiché la frequenza di risonanza in cassa sarà sempre superiore a quella in aria libera, dalla [2] sappiamo infatti che il minimo Qmb che potremo ottenere sarà proprio il Qms, e per quanto abbiamo detto sulla «nuova costante universale» sappiamo anche che sarà proprio il Qmb ottenuto a governare lo smorzamento finale, a prescindere dalla linearità che riusciremo a raggiungere sul modulo della risposta. Inoltre dobbiamo fare i conti con il volume di carico, perché se con volumi troppo piccoli la Fb sale troppo otterremo comunque risposte troppo poco estese verso il basso. Dobbiamo quindi citare una nuova relazione, anch’essa ben nota agli autocostruttori, ovvero
[3] (Fb/Fs)2 = Vas/Vb+1
dalla quale risulta che, a parità di incremento della risonanza in cassa (Fb) rispetto a quella in aria (Fs), il volume che determina tale incremento (Vb) è proporzionale al Vas (volume acustico equivalente alla cedevolezza delle sospensioni), ovvero che, a parità di volume di carico, la risonanza di un woofer dal Vas basso salirà meno di quella d’un woofer dal Vas alto. In linea di massima, i woofer più adatti ad essere pilotati in corrente saranno perciò caratterizzati da:
- Bassa Fs.
- Basso Vas.
- Basso Qms e basso rapporto Qms/Qts (il che equivale ad un picco d’impedenza alla risonanza poco pronunciato). Questa prerogativa è la sola rilevante nel caso che l’altoparlante da pilotare in corrente non sia un woofer.
Ingegneristicamente parlando, talune di queste esigenze sono in parte antitetiche.
Una bassa Fs può ad esempio essere ottenuta spingendo ad alti valori la cedevolezza delle sospensioni, il che però rende alto il Vas, e poiché l’alternativa (l’aumento della massa mobile) è economicamente svantaggioso in generale gli altoparlanti con la Fs più bassa sono anche quelli con il Vas più alto. Ciò non significa che il current drive sia difficilmente praticabile, ma solo che non è facile ottenere elevate estensioni in volumi piccoli. Se però in vece che ai soli altoparlanti dichiarata mente «home» guardiamo ad alcuni woofer per uso in autovettura, troveremo modelli con Vas basso e risonanze pure molto basse. In ambito «car» sussiste infatti l’esigenza di rendere le prestazioni il più possibile invarianti rispetto ai volumi di carico, e la prima regola da seguire per ottenere tale risultato è quella di rendere la cedevolezza del gruppo mobile poco dipendente dall’aria e molto dalle sospensioni.
Il problema della sensibilità
Per «sensibilità» di un filtro si intende la deriva della sua Fs rispetto alle variazioni dei valori nominali dei componenti che lo realizzano, dovuta alle tolleranze di produzione, alla temperatura, all’invecchiamento, etc. Un filtro è tanto meno sensibile quanto più stabile risulta essere la sua funzione di trasferimento rispetto alle variazioni dei valori dei componenti, e nella scorsa puntata abbiamo visto come il CVCD (Constant Voltage Current Drive, pilotaggio in corrente a «tensione costante») abbia in questa caratteristica un tallone d’Achille, perché operando sul principio della perfetta sintonia di stadi passa-banda (quello RLC equivalente all’impedenza dell’altoparlante e quello di compensazione) bastano deviazioni anche di poche unità percentuali nei componenti, oppure (e queste sono inevitabili) piccole modifiche nel tempo delle risonanze fondamentali dei trasduttori, per produrre alterazioni di non poco conto nella risposta. In fig. 6 vediamo cosa succede all’altoparlante più «ostico» esaminato nella scorsa puntata (Qtb in cassa con pilotaggio in tensione pari ad 1, Qmb pari a 5, Fb 150 Hz) utilizzato in un allineamento elettromeccanico già piuttosto complesso (Chebyschev del V ordine con ripple 0.71 dB ed F, 220 Hz) la cui parte elettronica risulta, come allora, starata del 3% sulla sola frequenza di taglio: oltre ad essere minori, le variazioni sul modulo e sulla fase della risposta acustica finale sono molto più graduali, e soprattutto interessano una parte molto limitata della banda passante (in questo caso estesa fino a circa 145 Hz).
Tecniche di «current drive» alternative
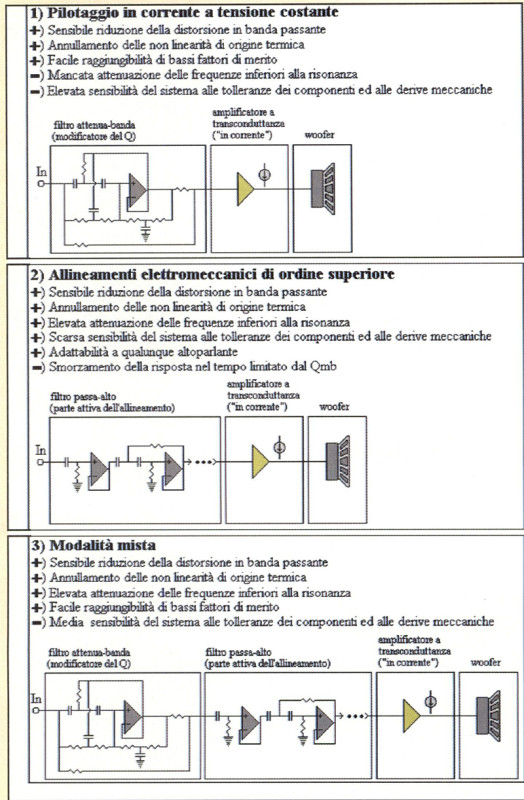
Una prima alternativa alla realizzazione degli allineamenti elettromeccanici in corrente di tipo «puro», ovvero basati sul ricorso a soli stadi passa-alto da far precedere all’amplificatore a transconduttanza, è quella degli allineamenti elettromeccanici basati sul CVCD (v. fig. 7). Supponiamo ad esempio di montare un altoparlante in un box tale da portare il suo Qtb con il normale pilotaggio in tensione ad un valore di 0.54. Se usiamo il CVCD riotterremo lo stesso Qtb, ma con i vantaggi e gli svantaggi (l’aumento della distorsione al di sotto della risonanza) propri del pilotaggio in corrente. Se però inseriamo il sistema così ottenuto all’interno di un Butterworth di ordine 4 (scindibile in due stadi di secondo ordine, uno di Q pari a 0.54 e l’altro di Q pari a 1.31), ovvero facciamo precedere (o seguire) allo stadio attenua-banda un filtro passa-alto del secondo ordine con Q=1.31 (ed Ft pari alla frequenza di risonanza in cassa) otterremo sia una risposta corretta che la piena soddisfazione del vincolo fondamentale per il progetto di un sistema pilotato in corrente (l’attenuazione delle frequenze inferiori alla risonanza). Una ulteriore variante di questo «mixed mode» potrebbe prevedere l’uso di un filtro attenua-banda atto non a consegnare una risposta piatta all’altoparlante (ovvero a tornare alla risposta del pilotaggio in tensione), ma solo a modificarne opportunamente il Q acustico.
Una seconda alternativa è quella di modificare la funzione di trasferimento acustica con una equalizzazione attiva, o mantenendo il secondo ordine acustico (provvedendo cioè ad alterare il fattore di merito ed eventualmente la frequenza di taglio dell’altoparlante in cassa chiusa pilotato in corrente), o cambiando addirittura ordine. Si tratta di tecniche sviluppate da alcuni «grandi» dell’elettroacustica (quali Siegfried Linkwitz e Marshall Leach) ma in relazione ad applicazioni convenzionali, basate sul pilotaggio in tensione: senza scendere nel dettaglio (altri menti ci occorrerebbero altre 10 pagine di rivista) diremo che nel primo caso (laddove implementabile) non viene rispettata l’esigenza di attenuare le frequenze inferiori alla risonanza, ed anche nel secondo, applicabile solo ove il Q del woofer non ecceda il valore di 1.31, si ottiene comunque una estensione della risposta in ragione del rapporto 1.31/Q. Trascuriamo in vece del tutto, perché richiederebbero (e forse richiederanno…) una trattazione autonoma, le tecniche basate sulla contro reazione acustica.
Peculiarità del pilotaggio in corrente
Esiste un vantaggio se condario del current drive che forse per un esoterista non è del tutto tale: l’annullamento dell’influenza dei cavi di collegamento, almeno per quanto riguarda l’influenza diretta sul segnale da questi trasportato (nel corso delle ricerche sulle interazioni deboli abbiamo infatti constatato come gli effetti di radiazione legati alla circolazione di corrente ed alla presenza di tensioni siano tutt’altro che trascurabili). Se l’amplificatore a transconduttanza è ben realizzato la corrente è del tutto indipendente dal carico, e vieppiù lo è dalle piccole variazioni di impedenza legate alla natura dei cavi di collega mento e relativi contatti.
C’è poi un aspetto insolito proprio del pilotaggio in corrente, ed è l’apparente mancanza di controllo delle membrane quando si cerca di spostarle manualmente.
Mentre infatti un altoparlante pilotato in tensione è smorzato «passivamente», ovvero i suoi movimenti sono ostacolati dalle correnti associate alle forze controelettromotrici indotte dal movimento della bobina nel traferro, nel caso del pilotaggio in corrente il controllo è quasi tutto «attivo»: la risposta del filtro correttore «precorregge» quella puramente acustica. Ma ciò comporta anche che ogni stimolo non proveniente dal circuito elettrico, quale appunto una sollecitazione diretta delle membrane, non ha modo di essere riconosciuto in quanto tale e non può quindi essere smorzato se non dal solo circuito meccanico. Questo effetto, se da un lato potrebbe lasciar pensare ad un minore
sfruttamento dell’escursione dell’altoparlante in condizioni operative (del tutto trascurabile però all’atto pratico), dall’altro offre però il vantaggio (altrettanto accademico) di non costringere l’amplificatore a cortocircuitare tutte le FEM indotte dalla pressione acustica non generata dall’altoparlante stesso.
Conclusioni
Abbiamo presentato due possibili tecniche di pilotaggio in corrente degli altoparlanti dinamici caricati da un volume chiuso, implementabili con semplici filtri elettronici. Attraverso tali metodologie è possibile abbassare notevolmente la distorsione acustica degli altoparlanti all’interno della banda passante, è possibile eliminare completamente tutte le degenerazioni di origine termica e (limitatamente alla seconda tecnica) ridurre fortemente l’escursione dell’equipaggio mobile per frequenze inferiori alla banda riproducibile. Come tutte le possibili varianti di pilotaggio in corrente anche quelle da noi proposte spingono facilmente il progettista verso la multiamplificazione e sia il costo relativamente elevato che consegue a tale soluzione, sia l’obbligo di creare sistemi amplificazione/altoparlanti di tipo integrato, la rendono appetibile soprattutto per catene audio di alto livello qualitativo; del resto, la necessità di montare l’altoparlante in un volume isolato non lascia certo propendere per applicazioni di tipo professionale, anzi, al contrario, proprio la raffinatezza acustica del caricamento a sospensione pneumatica (nessun problema di risonanze dei condotti o di turbolenze, qualità dinamiche ed acustiche legate a leggi lineari, etc.) ne rafforza la candidatura per applicazioni di punta.
L’autore di questo lavoro spera, con esso, di contribuire a muovere le acque stagnanti della ricerca di base in campo audio. Se infatti continueremo ad attribuire importanza capitale a dettagli la cui stessa sussistenza non è mai stata oggettivamente dimostrata, se molti progettisti continueranno a blandire le fissazioni degli audiofili non tecnici anziché dimostrargli (con il suono delle loro realizzazioni) che le catene audio hanno punti deboli ben determinati, in pratica gli stessi da sempre, allora probabilmente, tra una decina d’anni, ci ritroveremo ad operare sempre con le stesse tecnologie. E con molti appassionati in meno.
box di approfondimento
Un caso concreto
Supponiamo di avere effettuato uno screening di massima degli altoparlanti che riteniamo essere adatti ad un pilotaggio in corrente in sospensione pneumatica sulla base delle indicazioni fornite all’interno dell’articolo, e di aver selezionato il Peerless RS-60, le cui prestazioni con il pilotaggio in corrente abbiamo esaminato nella precedente puntata. Questo altoparlante parte con un Qms e Vas abbastanza bassi (2.2 e 29.5 litri), quindi dovrebbe essere versato per i nostri scopi, anche perché, nonostante il diametro ridotto (133 mm effettivi), l’elevata escursione massima (±5.5 mm) dovrebbe garantire una discreta dinamica anche con il «delicato» caricamento pneumatico.
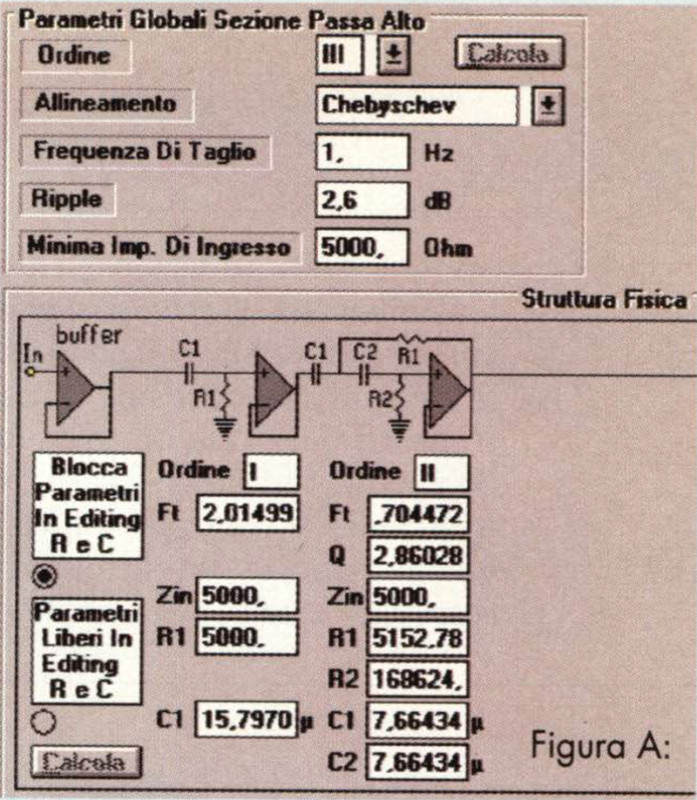
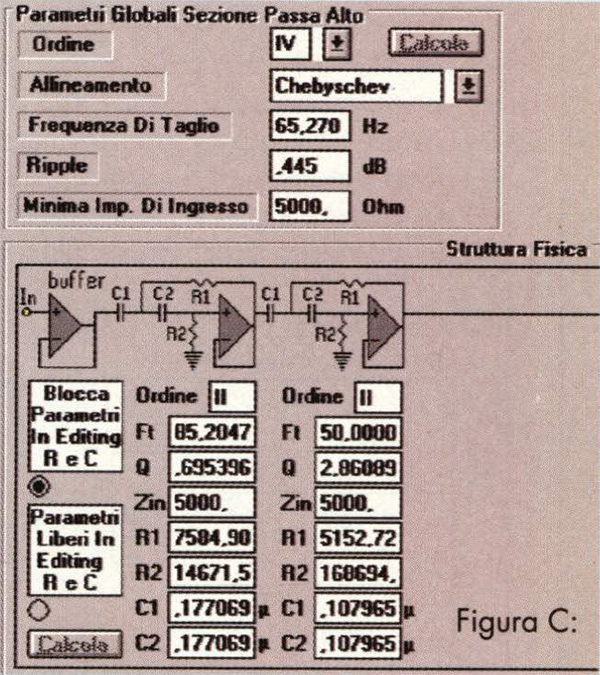
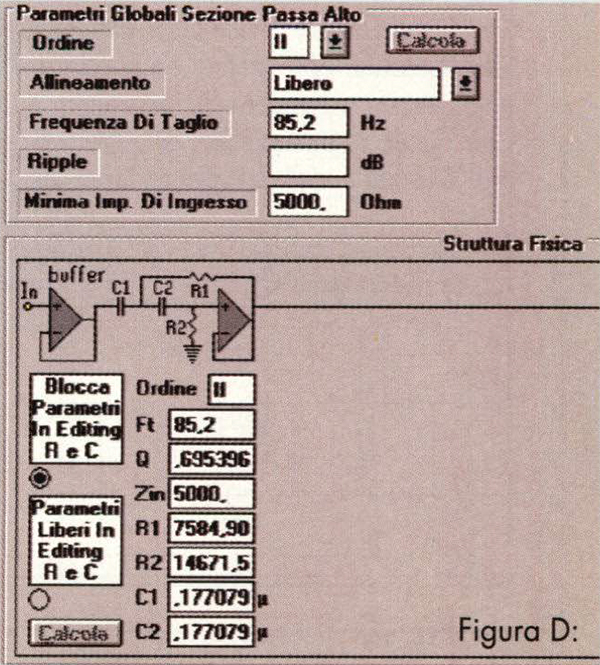
Supponiamo di voler ottenere una estensione di risposta fino a 50 Hz: Win-Bass alla mano, dovremo caricarlo in 43.4 litri (stiamo parlando di una cassa priva di perdite, per semplificare il discorso), ed otterremo di conseguenza un fattore di merito meccanico (Qmb) pari a 2.86, che è l’unico fattore di merito attivo con il pilotaggio in corrente. E se avessimo usato un programma di simulazione che non fornisce il Qmb ma solo il Qtb, ovvero il Q in cassa con il convenzionale pilotaggio in tensione? Semplicissimo, avremmo dovuto moltiplicare il Qtb per il rapporto Zm/Re, che rappresenta il coefficiente di «peggioramento» dello smorzamento totale quando si passa dal pilotaggio in tensione a quello in corrente. E se il programma di simulazione del caricamento non lo avessimo proprio? Allora avremmo dovuto applicare la [2], ed avremmo ottenuto il medesimo risultato. Cosa ci facciamo con un sistema dal Q pari a 2.86, che alla F, presenta un’enfasi di oltre 9 dB? Se volessimo realizzarci un allineamento di Bessel, le cose sarebbero un po’ complicate, bisognerebbe salire oltre il quindicesimo ordine (!!!), ma anche con Butterworth non sarebbero tanto semplici, perché per trovare un Q simile (per la precisione 2.88) dovremmo salire fino ad ordine 9. Inoltre in nessuno di questi casi WinCross 1.0 potrebbe esserci di ausilio, perché il massimo ordine da questi calcolato è il VI (che ragionevolmente è anche il massimo che si possa tentare di utilizzare in pratica). Abbiamo due alternative: o aumentiamo il volume di carico, e scendiamo con risonanza e Q meccanico, oppure dobbiamo rivolgerci ai Chebyschev. Per non compromettere la dinamica (stiamo pur sempre parlando di un altoparlante da 7 pollici) scegliamo di seguire la seconda strada, ed a questo punto le possibilità sono numerose. Aumentando opportunamente il ripple, un allineamento di Chebyschev richiede uno stadio di secondo ordine di Q qualsiasi anche con il semplicissimo terzo ordine. In questo caso, giocando un po’ con WinCross, troveremo che un passa-alto (ma il discorso sarebbe identico con un passa-basso) Chebyschev di ordine 3 richiede un Q=2.86 per l’unico stadio di secondo ordine quando il ripple vale 2.6 dB (v. fig. A): sono decisamente un po’ troppi per un diffusore ad alta fedeltà! Tentiamo quindi con il quarto ordine e le cose si mettono subito meglio, perché (fig. B) bastano 0.44 dB per poter inserire uno stadio di Q pari a 2.86; per mera curiosità, diremo che con il quinto ordine il ripple si riduce a 0.038 dB e con il sesto si arriva a 0.0012. Avrete notato che nei due tentativi effettuati abbiamo impostato per 1 filtri una frequenza di taglio globale di 1 Hz: ciò perché in tal modo nella casella «Fi» dei singoli stadi comparirà direttamente la frequenza di taglio normalizzata (il rapporto tra la frequenza di taglio del singolo stadio e quella globale) dei medesimi in quel particolare allineamento. Per calcolare allara quale frequenza di taglio globale dovremo attribuire al filtro dovremo rapportare la F, del diffusore, ovvero la frequenza di risonanza in cassa (Fb, che in questo caso avevamo fissato a 50 Hz), alla frequenza di taglio normalizzata (Fn) dello stadio: nello specifico, lo stadio con Q=2.86 ha una Fn=0.7ó6, sicché la frequenza di taglio globale da impostare varrà 50/.766=65.27 Hz. In fig. C vediamo l’assetto finale dell’allineamento, in cui il secondo stadio rappresenta la parte acustica, alias l’altoparlante montato nel suo box. Per realizzare il corretto allineamento Chebyschev del IV ordine, con ripple 0.44 dB ed F, 65.27 Hz (attenzione, solo nei Butterworth la F, coincide con la frequenza a -3 dB!), basterà far precedere all’amplificatore a transconduttanza il singolo stadio del secondo ordine di fig. D. Quella che otterremo sarà la risposta acustica di fig. E, che scende ai 3 dB a circa 48 Hz.
Tecniche attuative per il pilotaggio in corrente
di Fabrizio Montanucci
tratto da AUDIOreview n. 158 marzo 1996

![Pilotaggio in corrente degli altoparlanti [parte 2]](https://www.audioreview.it/wp-content/uploads/tecnica/pilotaggio-corrente-2.html/apertura.jpg)