Teoria e pratica dei filtri digitali

Nonostante i primi studi sui filtri digitali risalgano alla fine degli anni ’40 e, con la diffusione dell’audio digitale, il loro impiego sia ormai largamente diffuso anche in ambiente domestico, il loro principio di funzionamento è scarsamente noto al di fuori dell’ambito specialistico.
Questa serie di articoli si propone di introdurre all’attenzione degli appassionati e dei professionisti i principali aspetti teorici e applicativi connessi con l’impiego e l’utilizzazione nell’audio dei filtri digitali.

Introduzione

Nella storia dell’alta fedeltà, l’introduzione del compact disc è senz’altro stata una tappa fondamentale nella cosiddetta «rivoluzione digitale». Con la comparsa dei primi gira-dad dotati di uscita numerica, questa rivoluzione coinvolgerà ben presto tutta la catena di riproduzione hi-fi, a cominciare proprio dal preamplificatore, che in veste digitale diventerà un vero e proprio «elaboratore audio». Infatti, oltre ai classici controlli di selezione degli ingressi, di tono (naturalmente tutti numerici) e di volume (in tutto o in parte numerico), il pre digitale sarà in grado di equalizzare nel dominio del tempo e potrà contenere, come opzione, anche il crossover (digitale), rendendo così digitale tutto il sistema sino ai finali di potenza (fig. 1).

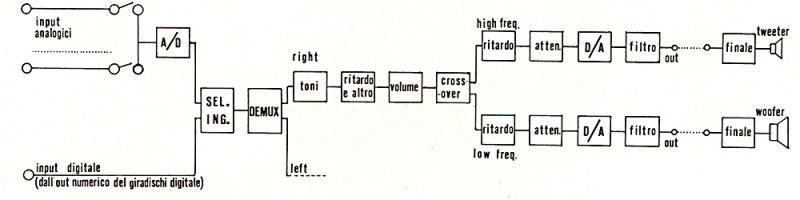
Figura 1 – Schema a blocchi di un preamplificatore digitale completo di crossover.

L’analisi dettagliata dei vari blocchi che costituiscono la struttura di un pre digitale sarà appunto l’argomento di una serie di articoli che verranno  pubblicati sulle pagine di questa rivista e che si concluderà con la presentazione di una rete di crossover digitale, della quale è stata da noi realizzata un prototipo funzionante. A questo proposito cogliamo l’occasione per ringraziare Paolo Nuti e Renato Giussani per il loro incoraggiamento e per l’aiuto da loro prestatoci.

Scheda SPU/02 sviluppata dal gruppo di ricerca della SIM (Società
d’Informatica Musicale) di Roma ed utilizzata dagli autori per la
implementazione della rete di crossover digitale citata nel testo.

Elaborazione numerica dei segnali

Un crossover digitale, al pari del suo omonimo analogico, è costituito ovviamente da un certo numero di filtri selettivi in frequenza. La differenza fondamentale tra un filtro digitale ed uno analogico risiede nel fatto che nel primo caso il segnale da elaborare non è un segnale continuo, bensì un segnale numerico, ovvero una sequenza di parole di b bit ciascuna (nel caso dell’audio digitale domestico, b= 16).

Tale sequenza è il risultato del campionamento e della quantizzazione del segnale acustico originale, che è di natura analogica. Questa operazione viene effettuata, come è noto, da un dispositivo chiamato «convertitore analogico – digitale» o «ADC» (dall’inglese Analog to Digital Converter). L’operazione di conversione ha inizio con la misura ed intervalli di tempo regolari del valore del segnale analogico di ingresso che viene memorizzato fino al successivo campione. Questa operazione è detta in inglese «sample and hold», vale a dire campionamento e memorizzazione (fig. 2).

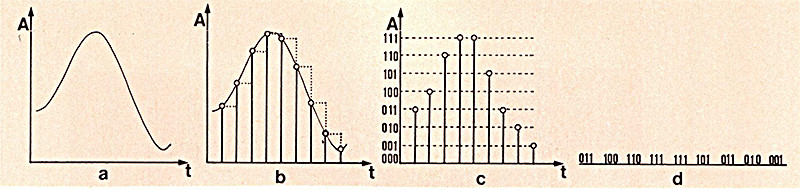
Figura 2 – Schema completo della conversione A/D: a) segnale analogico originale: b) campionamento e memorizzazione («sample and hold»): e) quantizzazione dei livelli: d) sequenza numerica di uscita.

Affinchè il segnale campionato mantenga inalterata la quantità di informazione originale, è necessario che la frequenza di campionamento, cioè il numero di campionamenti al secondo, sia maggiore od uguale al doppio della banda passante dei segnali di ingresso (nello standard dell’hi-fi digitale, la frequenza di campionamento è pari a 44.100 Hz). Poiché ogni campione può assumere qualsiasi valore, in quanto uguaglia il valore del segnale di ingresso ad un certo istante, la sequenza di campioni è ancora un segnale analogico.

Occorre quindi operare una discretizzazione dei valori che i campioni possono assumere, operando una approssimazione al più vicino livello lecito (quantizzazione dei livelli). Un b bit a disposizione, numero dei livelli leciti è pari a 2b-l ; se b= 16 si hanno 65.535 livelli. Per ultimare il processo di conversione, non resta che codificare i valori ottenuti in forma binaria: il segnale analogico originale si è così trasformato in una sequenza di parole a b bit.

È facile intuire che, essendo i segnali di ingresso e di uscita di un filtro digitale dei numeri, il funzionamento di questo sarà basato su una elaborazione numerica, cioè su un appropriato algoritmo di calcolo, che trasformi la sequenza di parole di ingresso X(n) in una sequenza di uscita Y(n). (Fig. 3).

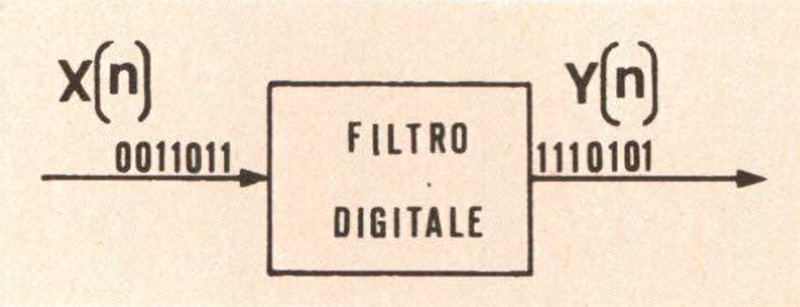
Figura 3 – «Blocco» filtro digitale, che trasforma una sequenza numerica d’ingresso X(n) in una sequenza d’uscita Y(n), che rappresenta la versione «filtrata» della precedente.

Prima di esaminare un vero e proprio processo di filtratura numerica è bene soffermarsi su alcuni esempi di elaborazione più semplici, che possano gradualmente mettere in evidenza le caratteristiche di questi processi.

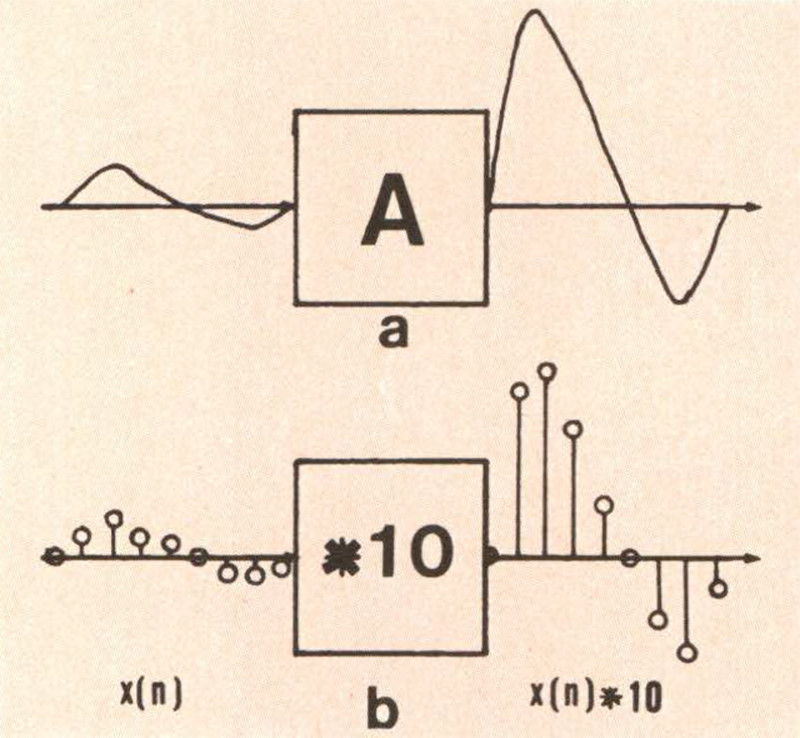
Figura 4 – a) Amplificatore analogico: b) amplificatore  numerico.

In figura 4 è mostrato lo schema di un amplificatore analogico con guadagno pari a 20 db (che amplifica cioè 10 volte il segnale d’ingresso). Lo stesso amplificatore in versione digitale può essere rappresentato come un blocco che moltiplica ogni campione della sequenza d’ingresso per 10:

Y(n)=10*X(n).

Si intuisce facilmente che il blocco di elaborazione potrebbe essere un comune microprocessore che esegua un piccolo programma consistente in tre semplici istruzini: a) input del campione; b) moltiplicazione del campione per IO; e) output del prodotto.

Affinchè il processo possa essere eseguito correttamente, le tre operazioni citate devono avvenire in un intervallo di tempo inferiore al periodo di campionamento pari, nel caso dell’audio digitale per impieghi domestici di alta fedeltà, a 22,6 u.s.

La necessità di riuscire a compiere le operazioni in questo intervallo di tempo è il presupposto fondamentale dell’elaborazione «in tempo reale», che è quella necessariamente utilizzata nell’audio digitale; non sarebbe infatti tollerabile, in attesa del termine dei calcoli, una «pausa» tra un campione ed il successivo.

Osserviamo inoltre che tali operazioni derivano da un programma residente nella memoria del nostro micro-computer. Se tale programma viene cambiato, cambierà l’operazione compiuta, e, invece di una moltiplicazione, potremmo ad esempio effettuare una somma, o ambedue, oppure altre operazioni, e quindi modificare la «filtratura» operata sul segnale.

Questo significa che il risultato dell’opera zione compiuta dal blocco non dipende dalla struttura hardware come nel caso analogico, ma è «software-dipendente».

Filtri digitali

Entriamo ora nel campo dei filtri digitali con un altro esempio, e supponiamo che questa volta il blocco di elaborazione ese gua la seguente operazione:

Y(n) = X(n) + 0.5*X(n-l)    (I).

Questa volta il campione di uscita Y(n) è stato ottenuto, come indica l’espressione stessa, sommando al campione della sequenza entrante X(n) il campione sempre appartenente alla sequenza in ingresso, ma precedente all’attuale, moltiplicato per 0.5.

In definitiva, in questo secondo esempio, l’elaborazione comprende le seguenti operazioni: una somma, una moltiplicazione ed il ritardo di un campione («one simple delay»). Queste costituiscono la triade di operazioni digitali su cui si basano tutte le elaborazioni numeriche, anche le più complesse.

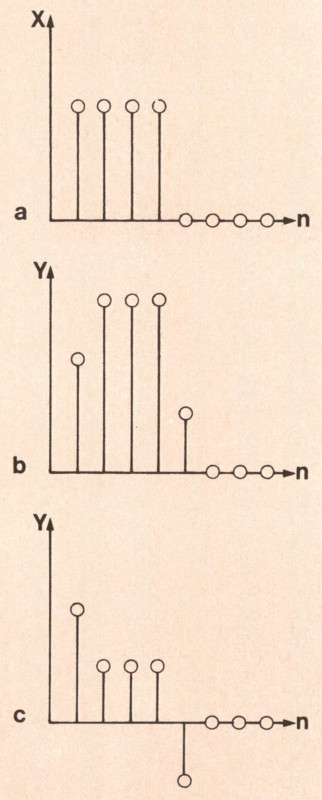
Figura 5 – a) Onda quadra campionato in in
gresso al filtro numerico; b) versione integra
ta dell’onda quadra; e) versione derivata del
l’onda quadra.

Torniamo al nostro esempio ed ipotizziamo un segnale d’ingresso costituito da un’onda quadra campionata come mostrato in fig. 5a. Come possiamo osservare, l’onda quadra in questione è stata campionata in modo da ottenere quattro campioni nella parte alta e quattro nella parte bassa. Eseguiamo l’operazione (I) campione dopo campione:
Y(0) = X(0) + 0.5*X(- 1)= 1 +0.5*0= 1
Y(l) = X(l) + 0.5*X(0) = 1+0.5*1 = 1.5
Y(2) = X(2) + 0.5*X(l)= 1 +0.5*1 = 1.5

Andando avanti si ottiene come sequenza di uscita quella mostrata nella figura 5b. È evidente dall’esame della figura stessa, che l’operazione compiuta ha avuto l’effetto di un filtro integratore (passa-basso).

Se proviamo ora ad invertire il segno nella formula (I) otteniamo l’espressione:

Y(n) = X(n)-0.5*X(n-l).

Ripetendo l’analogo procedimento numerico e riportando i risultati su un grafico (fig. 5c) ci accorgiamo che abbiamo realizzato un filtro derivatore (passa-alto).

Vediamo ora come si possa ottenere l’espressione di un processo di filtraggio di tipo molto selettivo, come ad esempio quello richiesto in un crossover. Iniziamo con alcune considerazioni di carattere generale, e più precisamente riprendendo il tema dei ritardi. Nelle espressioni precedenti è stato considerato i) ritardo di un solo campione, come dire che l’elaboratore doveva mantenere «da parte» solo il campione precedente a quello attuale. Vediamo ora qual è l’effetto di un «ritardatore» di m campioni, cioè di una elaborazione nella quale si utilizzi anche il campione che era entrato mintervalli di campionamento prima. Osserviamo innanzitutto che in questo caso, l’elaboratore dovrà disporre di un buffer di almeno m posizioni di memoria su cui mantenere ordinatamente tutti gli m campioni precedenti a quello attuale.

Nella letteratura relativa ai processi digitali dei segnali l’operazione di ritardo di m campioni viene indicato con il simbolo in dicato nella fig. 6. Con questa simbologia i due filtri esaminati negli esempi precedenti possono essere schematizzati come nella fig. 7.

Figura 6 – «Blocco» che opera il ritardo di m campioni.

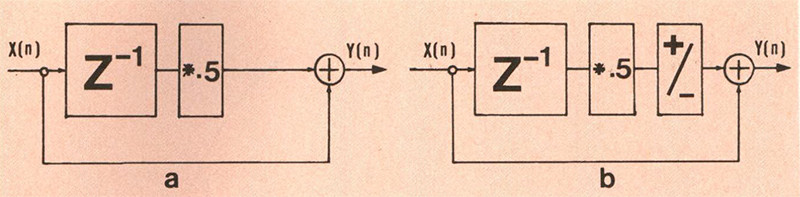
Figura 7 – a) Schema di funzionamento del filtro passa-basso Y(n)= X(n)+ 0.5*X(n— 1); b) schema di funzionamento del filtro passa-alto Y(n)= X(n)-0.5*X(n— 1).

Il «ritardatore» ha sostanzialmente l’effetto di un filtraggio particolare, detto «a pettine» (filtro comb), chiamato così perché presenta una risposta in frequenza del tipo mostrato in fig. 8a.

Figura 8 – a) Filtro «a pettine»; b) filtro selettivo infrequenza ottenuto da un filtro «a pettine».

Questa risposta è dovuta, del resto nel caso di un ritardo di tipo analogico, al fatto che ad alcune frequenze il segnale si trova in fase con se stesso mentre ad altre è in opposizione di fase. Possiamo ora pensare che, sommando al segnale l’ingresso più segnali ritardati ad hoc e moltiplicati per delle opportune costanti, alcuni dei poli e degli zeri causati dai vari segnali ritardati si annullino a vicenda, creando così un vero e proprio filtro selettivo in frequenza (fig. 8b).

È chiaro che per ottenere un filtro molto selettivo occorre sommare più ritardatori fino ad arrivare ad un m sufficentemente espressione che esprime l’operazione che deve compiere il nostro elaboratore per realizzare un filtraggio selettivo (fig. 9):

Y(n) = aoX(n) + AiX(n-l) + amX(n-m)   (II)

Supponiamo, per semplicità, m = 4 e che in ingresso al blocco che esegue l’operazione (II) vi sia un segnale come quello mostrato in fig. 9b (sequenza  impulso unitario).

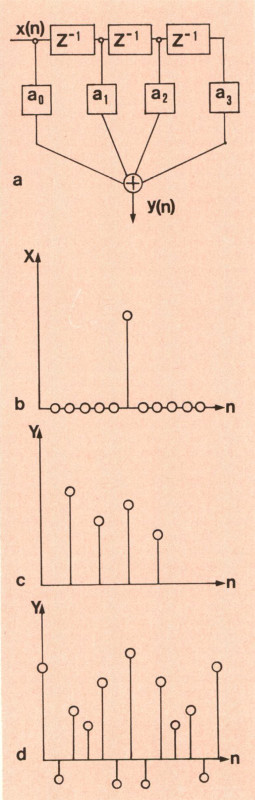
Figura 9 – a) Schema di funzionamento di
un filtro F.I.R. con tre celle di ritardo; b) sequenza impulso unitario; e) risposta del filtro F.I.R. di fig. 9a) alla sequenza impulso unitario; d) risposta di un generico filtro F.I.R. a fase lineare alla sequenza impulso unitario.

Quando arriva l’unico impulso costituente il segnale d’ingresso, i rami presenti nello schema daranno il loro contributo soltanto uno alla volta ed in successione, contributo che è pari al coefficente ai stesso. Avremo allora:

Y(O) = ao; Y(1) = a1; Y(2) = a2; Y(3) = a3.

Vista graficamente la risposta a questo impulso risulterà una sequenza di quattro impulsi uguali ai quattro coefficenti del filtro (fig. 9c). Questa risposta rappresenta la risposta impulsiva del filtro.

Balza subito agli occhi che, a differenza dei processi analogici, dove ad un ingresso impulsivo corrisponde una risposta non finita nel tempo, si ha in questo caso una risposta lunga soltanto quattro campioni. Di qui il nome di filtri con risposta impulsiva finita (F.I.R.: finit impulse response). Il progetto di un filtro F.I.R. è basato sulla determinazione della risposta impulsiva, quindi dei coefficenti. Le successive posizioni di ritardo sono dette «tappe».

Fra le varie strutture che può assumere la risposta impulsiva, sono particolarmente importanti quelle di tipo simmetrico (fig. 9d).

In questi casi, infatti, il filtro presenterà una risposta in fase lineare.

Analogamente a quanto succede in campo analogico, la conoscenza della risposta di un sistema numerico alla sequenza impulso unitario (risposta che indicheremo nel seguito con il simbolo h(n)) ci permette di ricavare la funzione di trasferimento del sistema stesso, e cioè sia la risposta in ampiezza che quella in fase.

Nel caso di filtri F.I.R. con m coefficenti la risposta in frequenza ha la forma:

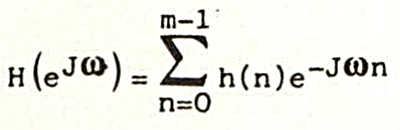
Il modulo della funzione H(e^Jω) rappresenta la risposta in ampiezza del filtro, mentre l’argomento ci dà la risposta in fase.
La notazione H(e^Jω) sta a significare che H è una funzione di ω, periodica con periodo 2π. La periodicità di H deriva evidentemente dal fatto che un segnale numerico proveniente da un convertitore analogico-digitale è sempre periodico, poiché comprende anche le «immagini» del segnale originale, con periodo pari a Tc=l/fc. In generale, però, nella teoria della elaborazione numerica dei segnali si preferisce usare come variabile indipendente, per motivi di semplicità, la pulsazione «normalizzata» ω = 2πf/fc, al posto della frequenza f, ed è per questo motivo che il periodo della nostra risposta H è pari a 2π. Accanto alle strutture F.I.R. che abbiamo ora esaminato, esistono altre strutture di filtri digitali, quali gli I.I.R. (infinite impulse response), caratterizzati dalla presenza di feedback tra uscita ed ingresso, e molto slmili, nel comportamento, ai filtri analogici. Una struttura tipica degli I.I.R. è mostrata nella fig. 10 nella quale si osserva che questa volta è il campione di uscita ad essere ritardato, prima di essere riportato in ingresso (nei filtri F.I.R. invece un campione di uscita dipende solo dal presente e dai precedenti campioni d’ingresso). Questo tipo di filtro presenta, da un lato il pericolo dell’instabilità, dall’altro non è possibile ottenere risposte di fase lineare, ed è per questi motivi che per le elaborazioni audio riteniamo più opportuno ricorrere a configurazioni F.I.R.

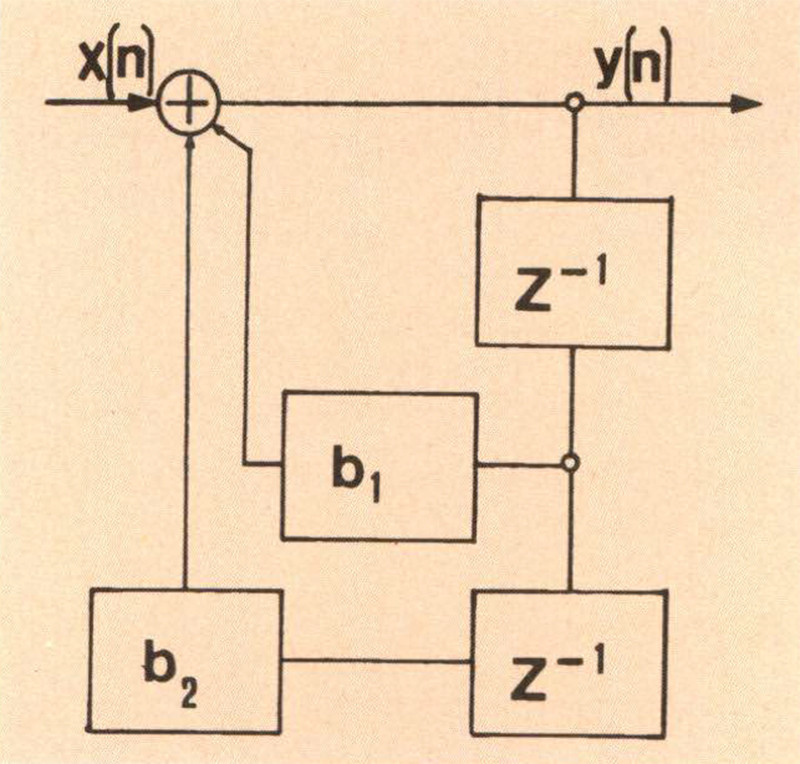
Figura 10 – Schema di funzionamento di un filtro I.I.R. con due celle di ritardo.

Progettazione di un filtro digitale

Vista quella che possiamo definire la struttura generale di un filtro digitale, vediamo ora come lo si possa progettare, partendo dapprima dalla definizione di un certo numero di specifiche di progetto per arrivare infine alle tecniche di progettazione vere e proprie, che hanno lo scopo di determinare i coefficenti (che non sono altro, se il filtro è un F.I.R., che i campioni della sequenza risposta alla sequenza impulso unitario!) che ne definiscono completamente la risposta. Le specifiche di progetto di un filtro digitale sono rappresentate nella maggior
parte dei casi da una maschera di tolleranza entro cui deve cadere la risposta del filtro (fig. 11).

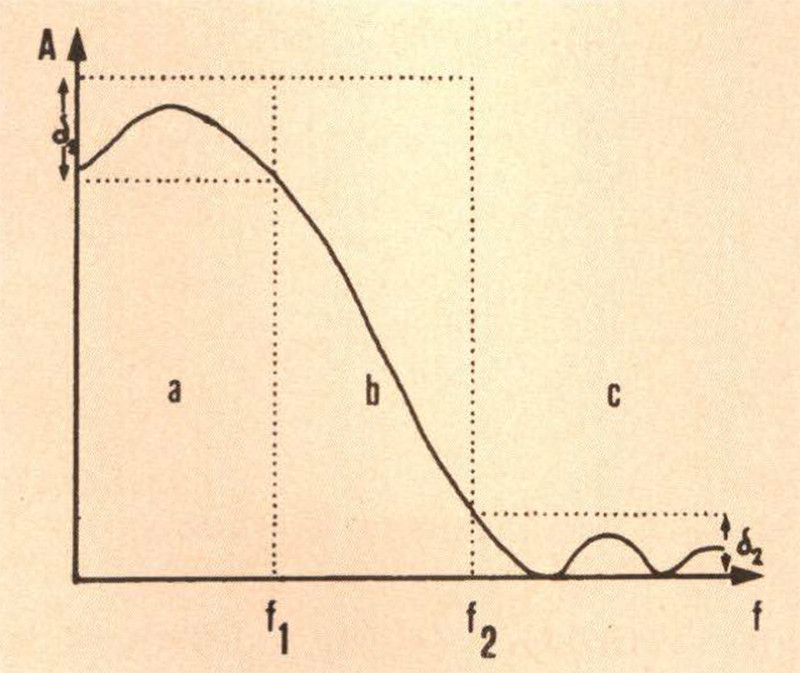
Figura 11- Maschera di tolleranza per la risposta in ampiezza di un filtro digitale: a) banda passante; b) banda di transizione; e) banda soppressa.

I dati iniziali di progetto consisteranno allora in due frequenze (fi, f2) che dividono la risposta in tre zone distinte (banda passante, banda di transizione, banda soppressa), in due valori limite δ1 e δ2 per il ripple (ovverosia l’ondulazione residua presente nella risposta del sistema) rispettivamente per la banda passante e per la banda soppressa, e naturalmente nel numero m di coefficenti del filtro. A parità di m, più vicine saranno fi e f2 e maggiore sarà la pendenza del taglio (che però, a differenza di quanto accade in un filtro analogico a fase minima, non è costante), ma maggiore sarà anche il ripple. Una volta decise le specifiche di progetto, e supponendo d’ora in poi di prendere in considerazione, per i motivi prima enunciati, solamente filtri F.I.R. a fase lineare non resta altro che determinare i valori dei coefficienti che permetteranno al filtro di soddisfare alle specifiche date. A tale proposito esistono diversi procedimenti, dei quali il più semplice da attuare (ed anche quello di più facile comprensione) è sicuramente il metodo «Windowing» (Finestratura).

Per capire il suo funzionamento, prendiamo come esempio la progettazione di un filtro passa-basso. Naturalmente, il «migliore» passa-basso teoricamente ipotizzabile è quello cosiddetto «ideale», mostrato in fig. 12. Chiamata con ωr = 2πft/fc la pulsazione «normalizzata» di taglio del filtro, la risposta in ampiezza di questo può esse re espressa in forma matematica come:
A(ω)= I per ω compresa tra 0 e ωT
A(ω) = 0 per ω maggiore di ωt

Figura 12 – Risposta in ampiezza A(ω) di un passa-basso ideale (tratto continuo) e risposta «periodizzata» A (ejω) dello stesso (tratto punteggiato).

Proviamo ora a pensare che tale risposta in ampiezza non sia altro che una parte di una funzione A (e^jω) periodica con periodo di
2π e pari (simmetrica cioè rispetto all’asse delle ampiezze) (fig. 12). Ma allora A(e^jω) può essere vista, come d’altronde tutte le funzioni periodiche aventi un numero finito di discontinuità, come la somma di un numero infinito di funzioni sinusolidali di diversa ampiezza e fase, che hanno frequenza pari o multipla alla frequenza fondamentale (che per semplicità, come abbiamo già spiegato, abbiamo posto uguale a 2π, ma che nella realtà corrisponde alla frequenza di campionamento fc).

In altre parole, la nostra risposta A(e^jω) può essere sviluppata in serie di Fourier, ottenendo come risultato:

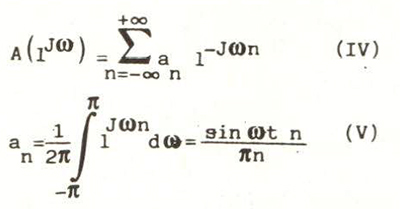
Salta subito agli occhi la somiglianzà tra la IV e la III, divergendo le due quantità solamente per gli estremi della serie: quindi la risposta in frequenza H(e^jω) di un filtro F.I.R. passa-basso uguaglia lo sviluppo in serie di Fourier, troncato però all’m-esimo termine, della funzione A(e^jω). Questo vale a dire che i campioni h(n) della risposta alla sequenza impulso unitario, cioè i coefficenti del filtro passa-basso cercati, non sono altro che i coefficenti dello sviluppo in serie di Fourier (troncato aH’m-esimo termine) della risposta passa-basso ideale «periodizzata», dati dalla relazione (V).

Purtroppo però la risposta del filtro così progettato divergerà sensibilmente dalla risposta «ideale», presentando delle sensibili «ondulazioni» a causa della troncatura all’m-esimo termine della serie di Fourier. Infatti, solamente con un numero infinito di coefficenti il nostro filtro diventerebbe «ideale»; ma, per definizione, un filtro F.I.R. ha una risposta all’impulso di durata finita, e quindi un numero finito di coefficenti. D’altra parte, è chiaro che un filtro F.I.R. con un numero infinito, o perlomeno elevatissimo, di coefficenti sarebbe impossibile da implementare.

Per ridurre l’ampiezza del ripple nella risposta del passa-basso, provocato appunto dalla troncatura del numero dei coefficenti, si ricorre alla tecnica della «finestratura», che consiste nel moltiplicare la sequenza dei coefficenti h(n) per un’altra sequenza w(n), detta appunto «window» («finestra»), operazione che accelera la convergenza della serie e diminuisce le ondulazioni della risposta (fig. 13).

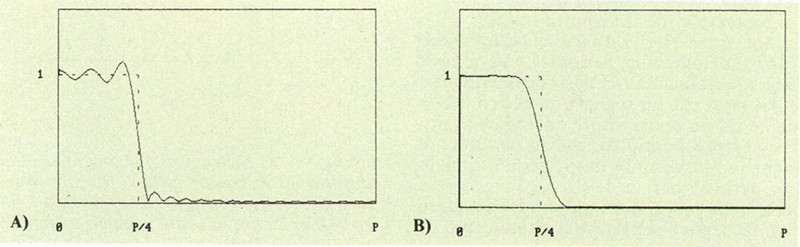
Figura 13 – a) Risposta di un filtro passa-basso con frequenza di taglio n/4 ottenuta con il metodo dello sviluppo in serie di Fourier; b) effetto della finestratura sulla risposta 13a.

Esistono vari tipi di finestre, tra cui possiamo ricordare due delle più usate, cioè quella «rettangolare» e quella «di Hamming», definite rispettivamente dalle sequenze:

Riassumiamo quindi quali sono le operazioni da compiere per giungere alla determinazione dei coefficenti di un filtro F.l.R. con il metodo della finestratura:

1. scelta del numero dei coefficenti
2. scelta della maschera d’ampiezza desiderata
3. determinazione dei valori dei coefficenti della serie di Fourier della risposta in ampiezza «periodizzata»
4. determinazione dei valori dei coefficenti della finestra
5. esecuzione del prodotto dei termini corrispondenti delle due sequenze.

Un programma in Basic che sfrutta questo metodo di progetto è mostrato in fig. 14, e in fig. 15 si possono vedere alcuni degli output grafici del programma stesso.

Figura 14 – Listato del programma in basic per IBM-compatibili per la ricerca dei coefficienti di un filtro F.l.R. con il metodo della finestratura, tratto da «Musica digitale» di L. Del Duca.

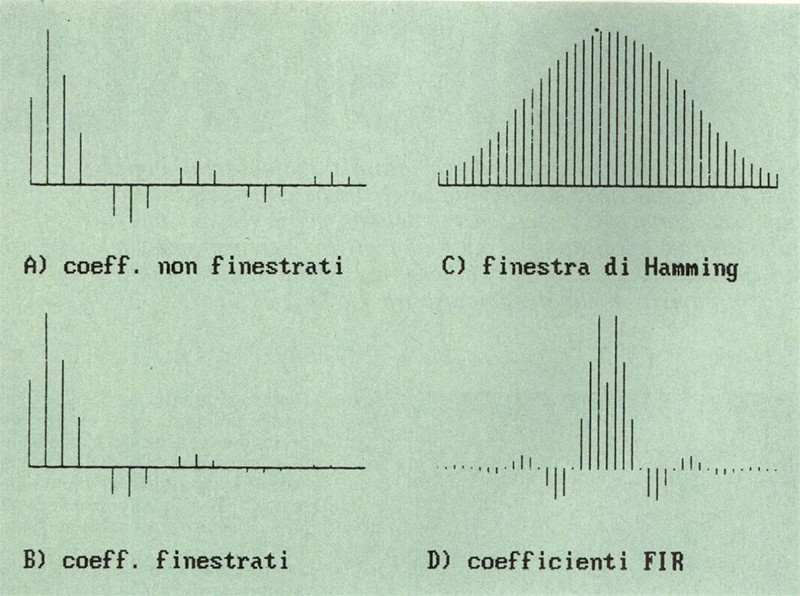
Figura 15 – Output grafico del programma.

Quando si voglia però progettare un filtro che sia il «migliore» ottenibile utilizzando un certo numero di coefficenti, occorre ricorrere a tecniche di progetto molto più complesse, la cui trattazione esula però dagli scopi di questo articolo. Basti per il momento sapere che tali tecniche si basano su procedimenti iterativi molto laboriosi, che variano continuamente i valori dei coefficenti del filtro fino ad arrivare alla migliore approssimazione del filtro ideale: questa, ad esempio è la tecnica che abbiamo seguito per la progettazione del nostro crossover
digitale.

È bene infine ripetere che, qualunque metodo di ricerca dei coefficenti si adotti, maggiore sarà il numero di coefficenti del filtro migliore sarà l’approssimazione del filtro ideale, ma più grandi saranno anche le difficoltà di implementazione, in quanto all’aumentare dei coefficenti aumenteranno anche il numero di somme e di prodotti che il filtro deve effettuare, e quindi aumenterà il tempo di calcolo necessario.

Conclusioni

II filtro digitale è il «blocco» che sta alla base di qualsiasi realizzazione audio digitale, compreso naturalmente il preamplificatore. Abbiamo visto come il suo funzionamento sia basato su algoritmi di calcolo che fanno uso di tre sole operazioni: somma, moltiplicazione, ritardo di campioni.

Nel prossimo articolo mostreremo come tali operazioni si realizzano praticamente, parleremo cioè dell’implementazione di un filtro digitale.

di Lindoro Massimo del Duca – Roberto Lucchesi – Rosaria Ferrarese

da AUDIOreview n. 51 giugno 1986

Bibliografia

• L.R. Rabiner – B. Golcl/ Theory And Application Of Digital Signal Processing/Prentice-Hall.
• A.V. Oppenheim – R.W. Shafer/Elaborazione numerica dei segnali/Franco Angeli Editore.
• L. Del Duca/Musica digitale/Muzzio Editore.